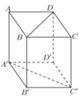
Cho hình lập phương ABCD.A’B’C’D’ có cạnh bằng a (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng BD và AC’ là
A. 3 a
B. a
C. 3 2 a .
D. 2 a .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 8 2019
Đáp án D.
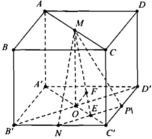
Gọi P là trung điểm của C’D’ suy ra d = d O ; M N P
Dựng:
O A ⊥ N P ; OF ⊥ ME ⇒ d=OF= M O . N E M O 2 + N E 2
trong đó
M O = a ; N E = a 2 4 ⇒ d = a 3 .
CM
22 tháng 8 2017
Ta có: d ( BD;A'C' ) = d ( BD;( A'B'C'D' )) = d ( B;( A'B'C'D' )) = BD' = a
Đáp án cần chọn là B
Đáp án B.
Gọi O là giao điểm của AC và BD, O’ là giao điểm của A’C’ và B’D’.
Ta có OO’//AA’ ⇒ OO ⊥ A B C D và OO ' ⊥ A ' B ' C ' D '
⇒ OO ' ⊥ B D OO ' ⊥ A ' C ' ⇒ OO ' là đoạn vuông góc chung của BD và A’C’
⇒ OO ' là khoảng cách giữa A’C’ và BD
⇒ d A ' C ' , B D = a .