Tính:
a) 6 3 1 : 6 2 1
b) 7 2 1 2 : 7
c) 2018 2 0 1 8 : 1 2018
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

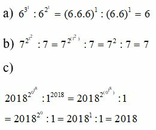

a) \(\dfrac{6}{7}+\dfrac{7}{8}=\dfrac{48}{56}+\dfrac{49}{56}=\dfrac{97}{56}\)
b) \(\dfrac{4}{5}-\dfrac{2}{3}=\dfrac{12}{15}-\dfrac{10}{15}=\dfrac{2}{15}\)
c) \(\dfrac{2}{3}.\dfrac{4}{9}=\dfrac{8}{27}\)
d) \(\dfrac{1}{5}:\dfrac{2}{7}=\dfrac{1}{5}.\dfrac{7}{2}=\dfrac{7}{10}\)
a: =48/56+49/56
=97/56
b: =12/15-10/15
=2/15
c: =(2*4)/(3*9)=8/27
d: =1/5*7/2=7/10

Bài 1.
\(a,\left(2^4\cdot3\cdot5^2\right):\left\{450:\left[450-\left(4\cdot5^3-2^3\cdot5^2\right)\right]\right\}\)
\(=\left(16\cdot3\cdot25\right):\left\{450:\left[450- \left(4\cdot125-8\cdot25\right)\right]\right\}\)
\(=\left(48\cdot25\right):\left\{450:\left[450-\left(500-200\right)\right]\right\}\)
\(=1200:\left[450:\left(450-300\right)\right]\)
\(=1200:\left(450:150\right)\)
\(=1200:3\)
\(=400\)
\(---\)
\(b,3^3\cdot5^2-20\left\{90-\left[164-2\cdot\left(7^8:7^6+7^0\right)\right]\right\}\)
\(=27\cdot25-20\left\{90-\left[164-2\cdot\left(7^2+1\right)\right]\right\}\)
\(=675-20\left\{90-\left[164-2\cdot\left(49+1\right)\right]\right\}\)
\(=675-20\left[90-\left(164-2\cdot50\right)\right]\)
\(=675-20\left[90-\left(164-100\right)\right]\)
\(=675-20\left(90-64\right)\)
\(=675-20\cdot26\)
\(=675-520\)
\(=155\)
\(---\)
\(c,\left[\left(18^7:18^6-17\right)\cdot2022-1986\right]\cdot5\cdot1^{2022}-13^2\cdot2020^0\)
\(=\left[\left(18-17\right)\cdot2022-1986\right]\cdot5\cdot1-169\cdot1\)
\(=\left(1\cdot2022-1986\right)\cdot5-169\)
\(=\left(2022-1986\right)\cdot5-169\)
\(=36\cdot5-169\)
\(=180-169\)
\(=11\)
Bài 2.
\(a) (2^x+1)^2+3\cdot(2^2+1)=2^2\cdot10\\\Rightarrow (2^x+1)^2+3\cdot(4+1)=4\cdot10\\\Rightarrow (2^x+1)^2+3\cdot5=40\\\Rightarrow (2^x+1)^2+15=40\\\Rightarrow (2^x+1)^2=40-15\\\Rightarrow (2^x+1)^2=25\\\Rightarrow (2^x+1)^2= (\pm 5)^2\\\Rightarrow \left[\begin{array}{} 2^x+1=5\\ 2^x+1=-5 \end{array} \right.\\ \Rightarrow \left[\begin{array}{} 2^x=4\\ 2^x=-6 (vô.lí) \end{array} \right. \\ \Rightarrow 2^x=2^2\\\Rightarrow x=2\)
Vậy \(x=2\).
\(---\)
\(b)3\cdot(x-7)+2\cdot(x+5)=41\\\Rightarrow 3\cdot x+3\cdot(-7)+2\cdot x+2\cdot5=41\\\Rightarrow 3x-21+2x+10=41\\\Rightarrow (3x+2x)+(-21+10)=41\\\Rightarrow 5x-11=41\\\Rightarrow 5x=41+11\\\Rightarrow 5x=52\\\Rightarrow x=\dfrac{52}{5}\)
Vậy \(x=\dfrac{52}{5}\).
\(Toru\)

a: \(=\dfrac{-7}{8}\left(\dfrac{3}{5}+\dfrac{2}{5}\right)+3+\dfrac{7}{8}=\dfrac{-7}{8}+\dfrac{7}{8}+3=3\)
b: \(=-\dfrac{8}{5}:\dfrac{5}{3}=-\dfrac{24}{25}\)
c: \(=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{3}{4}=\dfrac{6}{7}+\dfrac{1}{8}-\dfrac{6}{8}=\dfrac{6}{7}-\dfrac{5}{8}=\dfrac{48}{56}-\dfrac{35}{56}=\dfrac{13}{56}\)

a) Ta có: \(\dfrac{-5}{7}\left(\dfrac{14}{5}-\dfrac{7}{10}\right):\left|-\dfrac{2}{3}\right|-\dfrac{3}{4}\left(\dfrac{8}{9}+\dfrac{16}{3}\right)+\dfrac{10}{3}\left(\dfrac{1}{3}+\dfrac{1}{5}\right)\)
\(=\dfrac{-5}{7}\cdot\dfrac{3}{2}\cdot\dfrac{21}{10}-\dfrac{3}{4}\cdot\dfrac{56}{3}+\dfrac{10}{3}\cdot\dfrac{8}{15}\)
\(=\dfrac{-9}{4}-14+\dfrac{16}{9}\)
\(=\dfrac{-1621}{126}\)
b) Ta có: \(\dfrac{17}{-26}\cdot\left(\dfrac{1}{6}-\dfrac{5}{3}\right):\dfrac{17}{13}-\dfrac{20}{3}\left(\dfrac{2}{5}-\dfrac{1}{4}\right)+\dfrac{2}{3}\left(\dfrac{6}{5}-\dfrac{9}{2}\right)\)
\(=\dfrac{-17}{26}\cdot\dfrac{13}{17}\cdot\dfrac{-3}{2}-\dfrac{20}{3}\cdot\dfrac{3}{20}+\dfrac{2}{3}\cdot\dfrac{-33}{10}\)
\(=\dfrac{3}{4}-1-\dfrac{11}{5}\)
\(=-\dfrac{49}{20}\)

3: Số học sinh giỏi là 40*1/5=8 bạn
Số học sinh trung bình là 32*3/8=12 bạn
Số học sinh khá là 32-12=20 bạn
1:
a: -1/3+7/6=7/6-2/6=5/6
b: 5/7-3/5=25/35-21/35=4/35
c: 0,75*4/5=4/5*3/4=3/5

1.
a, => 21-x+3 < 0
=> 24-x < 0
=> x < 24
b, => 7+x > 0
=> x > -7
c, => x-1 < 0 ; x+2 > 0 ( vì x-1 < x+2 )
=> x < 1 ; x > -2
=> -2 < x < 1
Tk mk nha

A = 0-1 + 2-3 + 4-5 +...+ 2017-2018
=> A = (-1) + (-1) + (-1) +...+ (-1) (Có 1009 số hạng)
=> A = 1009.(-1)
=> A = -1009
B = 1-3+5-7+ 9-11+....+2005-2007
=> B = (-2) + (-2) +(-2) +...+ (-2) (Có 502 số hạng)
=> B = 502.(-2)
=> B = -1004
C=1+2+3-4-5-6+7+8+9-10-11-12+.....+97+98+99-100-101-102
=> C = (1+2+3-4-5-6)+...+(97+98+99-100-101-102) (có 17 cặp số)
=> C = (-9) + (-9) +...+ (-9) (có 17 số hạng)
=> C = (-9).17
=> C = -153

a) \(\dfrac{7}{8} + \dfrac{7}{8}:\dfrac{1}{8} - \dfrac{1}{2}\)
\(\begin{array}{l} = \dfrac{7}{8} + \dfrac{7}{8}.8 - \dfrac{1}{2}\\ = \dfrac{7}{8}.1 + \dfrac{7}{8}.8 - \dfrac{1}{2}\\ = \left( {\dfrac{7}{8}.1 + \dfrac{7}{8}.8} \right) - \dfrac{1}{2}\\ = \dfrac{7}{8}.\left( {1 + 8} \right) - \dfrac{1}{2} = \dfrac{7}{8}.9 - \dfrac{1}{2}\\ = \dfrac{{63}}{8} - \dfrac{1}{2} = \dfrac{{63}}{8} - \dfrac{4}{8} = \dfrac{{63 - 4}}{8} = \dfrac{{59}}{8}\end{array}\)
b) \(\dfrac{6}{{11}} + \dfrac{{11}}{3}.\dfrac{3}{{22}}\)
\(\begin{array}{l} = \dfrac{6}{{11}} + \dfrac{{11.3}}{{3.22}} = \dfrac{6}{{11}} + \dfrac{1}{2}\\ = \dfrac{{12}}{{22}} + \dfrac{{11}}{{22}} = \dfrac{{12 + 11}}{{22}} = \dfrac{{23}}{{22}}\end{array}\)

a)
\(\begin{array}{l}0,75 - \frac{5}{6} + 1\frac{1}{2} = \frac{3}{4} - \frac{5}{6} + \frac{3}{2}\\ = \frac{9}{{12}} - \frac{{10}}{{12}} + \frac{{18}}{{12}} = \frac{{17}}{{12}}\end{array}\)
b)
\(\begin{array}{l}\frac{3}{7} + \frac{4}{{15}} + \left( {\frac{{ - 8}}{{21}}} \right) + \left( { - 0,4} \right) = \frac{3}{7} + \frac{4}{{15}} - \frac{8}{{21}} - \frac{2}{5}\\ = \left( {\frac{3}{7} - \frac{8}{{21}}} \right) + \left( {\frac{4}{{15}} - \frac{2}{5}} \right)\\ = \left( {\frac{9}{{21}} - \frac{8}{{21}}} \right) + \left( {\frac{4}{{15}} - \frac{6}{{15}}} \right)\\ = \frac{1}{{21}} + \left( {\frac{{ - 2}}{{15}}} \right)\\ = \frac{5}{{105}} - \frac{{14}}{{105}}\\ = \frac{{ - 9}}{{105}} = \frac{{ - 3}}{{35}}\end{array}\)
c)
\(\begin{array}{l}0,625 + \left( {\frac{{ - 2}}{7}} \right) + \frac{3}{8} + \left( {\frac{{ - 5}}{7}} \right) + 1\frac{2}{3}\\ = \frac{5}{8} + \left( {\frac{{ - 2}}{7}} \right) + \frac{3}{8} - \frac{5}{7} + \frac{5}{3}\\ = \left( {\frac{5}{8} + \frac{3}{8}} \right) + \left( {\frac{{ - 2}}{7} - \frac{5}{7}} \right) + \frac{5}{3}\\ = 1 - 1 + \frac{5}{3} = \frac{5}{3}\end{array}\)
d)
\(\begin{array}{l}\left( { - 3} \right).\left( {\frac{{ - 38}}{{21}}} \right).\left( {\frac{{ - 7}}{6}} \right).\left( { - \frac{3}{{19}}} \right)\\ = \frac{{ - 3.\left( { - 38} \right).\left( { - 7} \right).\left( { - 3} \right)}}{{21.6.19}}\\ = \frac{{3.38.7.3}}{{21.6.19}}\\ = \frac{{3.2.19.7.3}}{{3.7.3.2.19}}\\ = 1\end{array}\)
e)
\(\begin{array}{l}\left( {\frac{{11}}{{18}}:\frac{{22}}{9}} \right).\frac{8}{5} = \left( {\frac{{11}}{{18}}.\frac{9}{{22}}} \right).\frac{8}{5}\\ = \frac{{11.9.4.2}}{{9.2.2.11.5}} = \frac{2}{5}\end{array}\)
g)
\(\left[ {\left( {\frac{{ - 4}}{5}} \right).\frac{5}{8}} \right]:\left( {\frac{{ - 25}}{{12}}} \right) = \frac{{ - 20}}{{40}}:\left( {\frac{{ - 25}}{{12}}} \right)\\ = \frac{{ - 1}}{2}.\frac{{ - 12}}{{25}} = \frac{6}{{25}}\)