Biết luôn có hai số a, b để F ( x ) = a x + b x + 4 ( 4 a - b ≠ 0 ) là nguyên hàm của hàm số f(x) và thỏa mãn 2 f 2 ( x ) = ( F ( x ) - 1 ) f ' ( x ) . Khẳng định nào dưới đây đúng và đầy đủ nhất?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Vì F(x) là nguyên hàm của hàm số ⇒ f x = F ' x
Ta có
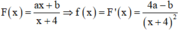

Khi đó
![]()

![]()
![]()
Phương trình (*) có nghiệm khi và chỉ khi a = 1 , b ∈ ℝ \ 4 .

- Vì F(x) và G(x) đều là nguyên hàm của f(x) nên tồn tại một hằng số C sao cho: F(x) = G(x) + C
- Khi đó F(b) – F(a) = G(b) + C – G(a) – C = G(b) – G(a).

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

F(x) là một nguyên hàm của hàm số f(x) => F'(x) = f(x)
Đồng nhất ta được 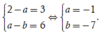
Chọn B.

Đáp án B
Ta có F x = x 2 + a x + b e - x ⇒ F ' x = - x 2 + 2 - a x + a - b e - x
mà f x = F ' x suy ra - x 2 + 2 - a x + a - b = - x 2 + 3 x + 6 ⇒ 2 - a = 3 a - b = 6 ⇔ a = - 1 b = - 7
Đáp án C