Cho hàm số y=f(x) có đạo hàm tại x0 là f’(x0). Khẳng định nào sau đây sai?
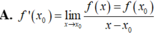
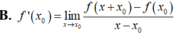
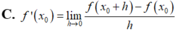

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+ Nếu hàm số y= f(x) có đạo hàm tại điểm x0 thì hàm số sẽ liên tục tại điểm x0
+ Ngược lại, nếu hàm số liên tục tại điểm x0 thì chưa chắc hàm số đã có đạo hàm tại điểm x0.
+ Theo định nghĩa đạo hàm tại 1 điểm ta có:
f ' ( x 0 ) = lim x → x 0 f ( x ) − f ( x 0 ) x − x 0 và f ' ( x 0 ) = lim Δ x → 0 f ( x 0 + Δ x ) − f ( x 0 ) Δ x
Vậy D sai
Chọn D.

A. Đúng (theo định nghĩa đạo hàm tại một điểm).
B. Đúng vì:
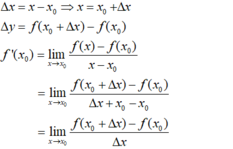
C. Đúng vì:
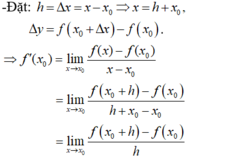
Chọn D

Đáp án D
- A. Đúng (theo định nghĩa đạo hàm tại một điểm).
- B. Đúng vì:
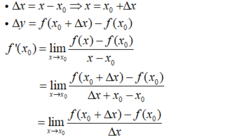
- C. Đúng vì:
+ Đặt:
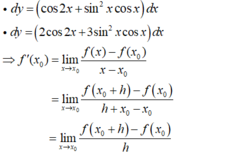

+ A đúng theo định nghĩa.
+ B đúng. Vì:
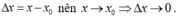
+ C đúng.
- Đặt:
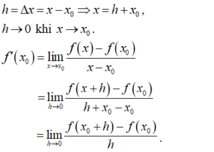
+ Vậy D sai.
Chọn D

Đáp án D
Câu C đúng theo điều kiện cần của cực trị.
Câu A, B đúng theo điều kiện đủ của cực trị. Câu D sai theo điều kiện đủ cho cực trị tồn tại