Giá trị của
A = 1 1 ! . 2018 ! + 1 2 ! . 2017 ! + 1 3 ! . 2016 ! + . . . + 1 1008 ! . 1011 ! + 1 1009 ! . 1010 ! bằng
A. 2 2017 - 1 2018 !
B. 2 2017 2018 !
C. 2 2017 2019 !
D. 2 2018 - 1 2019 !
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


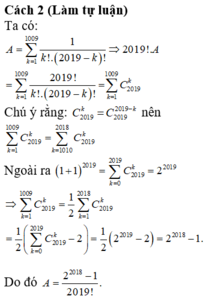

\(A=\frac{2018}{1}+\frac{2017}{2}+\frac{2016}{3}+...+\frac{1}{2018}\)
\(A=1+\left(1+\frac{2017}{2}\right)+\left(1+\frac{2016}{3}\right)+...+\left(1+\frac{1}{2018}\right)\)
\(A=\frac{2019}{2019}+\frac{2019}{2}+\frac{2019}{3}+...+\frac{2019}{2018}\)
\(A=2019\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2018}+\frac{1}{2019}\right)\)
Ta có: \(\frac{A}{B}=\frac{2019\left(\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2018}+\frac{1}{2019}\right)}{\frac{1}{2}+\frac{1}{3}+...+\frac{1}{2019}}=2019\)

C\(\frac{1}{1}-\frac{1}{2.3}+\frac{1}{3.4}-\frac{1}{4.5}+\frac{1}{5.6}\)-\(\frac{1}{6.7}\)+\(\frac{1}{7.8}\)-\(\frac{1}{8.9}+\frac{1}{9.10}\)
c=\(\frac{1}{1}-\frac{1}{10}\)
c=\(\frac{9}{10}\)
còn a và b rễ lắm mình ko thích làm bài rễ đâu bạn cố chờ lời giải khác nhé!



1) \(A=\frac{\left|x-2016\right|+2017}{\left|x-2016\right|+2018}=\frac{\left|x-2016\right|+2018-1}{\left|x-2016\right|+2018}=1-\frac{1}{\left|x-2016\right|+2018}\)
\(A\)nhỏ nhất nên \(\frac{1}{\left|x-2016\right|+2018}\)lớn nhất nên \(\left|x-2016\right|+2018\)dương nhỏ nhất.
mà \(\left|x-2016\right|+2018\ge2018\)
Dấu \(=\)khi \(x=2016\).
Vậy \(minA=1-\frac{1}{2018}=\frac{2017}{2018}\)đạt tại \(x=2016\).
2) \(x-2xy+y=0\)
\(\Leftrightarrow x\left(1-2y\right)+\frac{1}{2}-y-\frac{1}{2}=0\)
\(\Leftrightarrow\left(2x+1\right)\left(1-2y\right)=1=1.1=\left(-1\right).\left(-1\right)\)
Từ đây xét 2 trường hợp nha. Ra kết quả cuối cùng là: \(\left(x,y\right)\in\left\{\left(0,0\right),\left(1,1\right)\right\}\).

Nguyễn Tiến Đạt
a)\(|3x-5|=|x+2|\)
=> Ta có 2 trường hợp
*) TH1: 3x-5=x+2
=>3x-x=2+5
=>2x=7
=>x=7:2\(\Rightarrow x=\frac{7}{2}\)
*)TH2: -3x+5=x+2
\(\Rightarrow5-3x=x+2\)
\(\Rightarrow5-2=x+3x\)
\(\Rightarrow3=4x\)
\(\Rightarrow x=3:4\Rightarrow x=\frac{3}{4}\)
Vậy \(x\in\left\{\frac{7}{2};\frac{3}{4}\right\}\)

\(a^2+b^2+c^2=ab+bc+ac\)
\(a^2+b^2+c^2-ab-bc-ac=0\)
\(2\left(a^2+b^2+c^2-ab-bc-ac\right)=0\)
\(2a^2+2b^2+2c^2-2ab-2bc-2ac=0\)
\(\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(c^2-2ac+a^2\right)=0\)
\(\left(a-b\right)^2+\left(b-c\right)^2+\left(c-a\right)^2=0\)
mà \(\left(a-b\right)^2\ge0;\left(b-c\right)^2\ge0;\left(c-a\right)^2\ge0\forall a;b;c\)
\(\Rightarrow\hept{\begin{cases}a-b=0\\b-c=0\\c-a=0\end{cases}\Rightarrow\hept{\begin{cases}a=b\\b=c\\c=a\end{cases}\Rightarrow}a=b=c}\)
\(\Rightarrow\left(a-b+1\right)^{2018}+\left(b-c-1\right)^{2017}+\left(a-c\right)^{2016}\)
\(=\left(a-a+1\right)^{2018}+\left(c-c-1\right)^{2017}+\left(a-a\right)^{2016}\)
\(=1^{2018}+\left(-1\right)^{2017}+0^{2016}\)
\(=1+\left(-1\right)+0\)
\(=0\)
Vậy......
P.s: các phần thay a=b=c vào biểu thức có thể thay toàn bộ bằng a hoặc bằng b hoặc bằng c đều được nha