Cho a, b, c là ba số thực dương và khác 1. Đồ thị các hàm số y = log a x , y = log b x , y = log c x được cho trong hình vẽ bên.
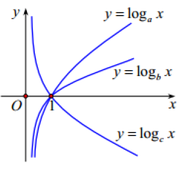
Mệnh đề nào dưới đây là mệnh đề đúng?
A. a < b < c
B. c < a < b
C. c < b < a
D. b < c < a
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hàm số \(y=log_cx\) nghịch biến
\(\Rightarrow0< c< 1\) và các hàm \(y=log_ax,y=log_bx\) đồng biến nên \(a,b>1\)
Ta chọn \(x=100\Rightarrow log_a>log_b100\Rightarrow a< b\Rightarrow b>a>c\)
\(\Rightarrow B\)

Khoảng giá trị của x mà đồ thị hàm số \(y=log_2x\) nằm phía trên đường thẳng y = 2 là \(\left(4;+\infty\right)\)
\(\Rightarrow\) Tập nghiệm của bất phương trình \(log_2x>2\) là \(\left(4;+\infty\right)\)

tham khảo.
Đồ thị của hai hàm số \(y=\log_ax\) và \(y=b\) luôn cắt nhau tại một điểm duy nhất. Khi đó phương trình \(\log_ax=b\) có nghiệm duy nhất \(x=a^b\).

Hàm số a,b là các hàm số logarit
a: \(log_{\sqrt{3}}x\)
Cơ số là \(\sqrt{3}\)
b: \(log_{2^{-2}}x\)
Cơ số là \(2^{-2}=\dfrac{1}{4}\)
Đáp án B
Hàm số y = log c x nghịch biến ⇒ 0 < c < 1 , các hàm y = log a x , y = log b x đồng biến nên a ; b > 1 Chọn x = 100 ⇒ log a 100 > log b 100 ⇒ a < b ⇒ c < a < b .