Cho hình chóp S.ABCD có S C = x 0 < x < a 3 , các cạnh còn lại đều bằng a. Biết rằng thể tích khối chóp S.ABCD lớn nhất khi và chỉ khi x = a m n m , n ∈ ℕ * . Mệnh đề nào sau đây đúng?
![]()
![]()
![]()
![]()
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn B.
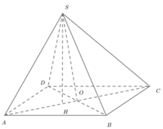
Phương pháp: Mấu chốt bài toán là chỉ ra được tam giác SAC vuông tại S.
Cách giải: Gọi O là giao điểm của AC và BD, H là hình chiếu của S lên mặt đáy.



Đáp án D

Gọi O = AC ∩ BD
Vì ABCD là hình thoi nên AC ⊥ BD tại O.
Tam giác SBD cân tại S nên SO ⊥ BD.
Suy ra BD
⊥
(SAC)![]()
Do ![]() => SO = OC
=> SO = OC![]()
![]()
![]()
![]()
![]()
![]()
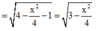
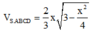
Đặt 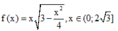
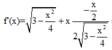
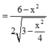
![]()
Bảng biến thiên:
| x |
0 |
|
|
+ 0 - |
|
|
|
Vậy ![]()

Đáp án D
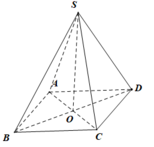

V S . A B C D = V S . A B C + V S . A D C = 2 V S . A B C = 2. 1 3 d B ; S A C S S A C = 2 3 x B O
O C = 1 2 A C = 1 2 S A 2 + S C 2 = 1 2 x 2 + 4 B O = B C 2 − O C 2 = 4 − x 2 4 − 1 = 3 − x 2 4 V S . A B C D = 2 3 x 3 − x 2 4
Đặt f ( x ) = x 3 − x 2 4 , x ∈ ( 0 ; 2 3 ]
f'(x)= 3 − x 2 4 + x − x 2 2 3 − x 2 4 = 6 − x 2 2 3 − x 2 4 f ' ( x ) = 0 ⇔ x = 6
Bảng biến thiên
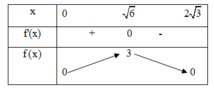
Vậy V max = 2 3 . max ( 0 ; 2 3 ] f ( x ) = 2 3 3 = 2

Chọn đáp án A
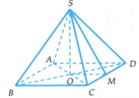
Gọi O là tâm của hình vuông ABCD, suy ra S O ⊥ A B C D
Gọi M là trung điểm của CD thì C D ⊥ O M mà C D ⊥ O M ⇒ C D ⊥ S O M
![]()
![]()
Đặt AB = 2x(x > 0) ⇒ O M = x
![]()
Do ∆ S O M vuông tại O nên S O = O M . tan S M O ⏜ = x . tan α
Do ∆ S O A vuông tại O nên S A 2 = S O 2 + O A 2
![]()
![]()
![]()
Thể tích khối chóp S.ABCD là
V S . A B C D = 1 3 S O . S A B C D
Ta có
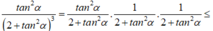
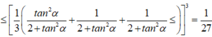
Suy ra 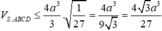
Dấu “=” xảy ra khi
![]()
![]()

Chọn D
H là tâm đường tròn nội tiếp đáy.
Cách giải: Vì góc hợp bởi đường cao SH của hình chóp và các mặt bên của hình chóp đều bằng α nên H là tâm đường tròn nội tiếp ABCD.
Vì các cạnh bên hình chóp S.ABCD bằng a nên H là tâm đường tròn ngoại tiếp ABCD.
Vậy ABCD là hình vuông. Suy ra S.ABCD là hình chóp tứ giác đều.
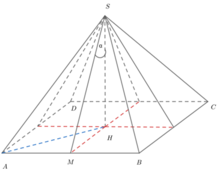
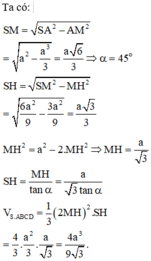
Đáp án A
Phương pháp:
+) Chứng minh hình chiếu vuông của S trên (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABD.
+) Chứng minh tam giác SAC vuông tại S, tính AC.
+) Tính BD.
+) Sử dụng công thức tính thể tích V S . A B C D = 1 3 S H . S A B C D = 1 3 S H . 1 2 A C . B D
Cách giải:
Vì SA = SB = SD = a nên hình chiếu vuông của S trên (ABCD) trùng với tâm đường tròn ngoại tiếp tam giác ABD.
Gọi H là tâm đường tròn ngoại tiếp tam giác ABD
⇒ S H ⊥ ( A B C D ) .
Do tam giác ABD cân tại A ⇒ H ∈ A C
Dễ dàng chứng minh được:
△ S B D = △ A B D ( c . c . c ) ⇒ S O = A O = A C 2 ⇒ △ S A C vuông tại S (Tam giác có trung tuyến ứng với một cạnh bằng nửa cạnh ấy)
Áp dụng hệ thức lượng trong tam giác vuông SAC có S H = S A . S C A C = a x a 2 + x 2
Ta có
Dấu “=” xảy ra