Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
hoc gioi the hihiihihihhhihihihihiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii
,mnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnnn
Đáp án: B
Giải bất phương trình - x + 2 x - 3 ≤ 0
Ta có bảng xét dấu vế trái của bất phương trình:
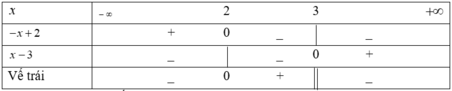
Vậy tập nghiệm của bất phương trình là: (- ∞ ;2] ∪ (3;+ ∞ )
Đáp án: B
Ta có:
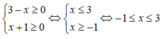
Vậy tập nghiệm của hệ bất phương trình là: [-1;3]
Đáp án C
f ( t ) = t ( t 2 + 3 + 1 ) ⇒ f ' ( t ) = t 2 + 3 + 1 + t t t 2 + 3 > 0 ∀ t ( x + 2 ) ( ( x + 2 ) 2 + 3 + 1 ) > − x ( x 2 + 3 + 1 ) ⇔ ( x + 2 ) ( ( x + 2 ) 2 + 3 + 1 ) > − x ( ( − x ) 2 + 3 + 1 ) ⇔ f ( x + 2 ) > f ( − x ) ⇔ x + 2 > − x ⇔ x > − 1
Chọn D.
Ta có
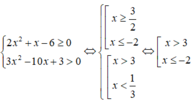
Vậy tập nghiệm hệ bất phương trình là S = ( - ∞ ;-2] ∪ (3; + ∞ ).
Chọn B.
Ta có:
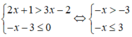
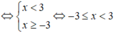
Tập nghiệm của hệ bất phương trình là S = [-3;3).
Đáp án B
Điều kiện x < 0 .
log π 4 log 2 x + 2 x 2 − x < 0 ⇔ log π 4 log 2 x + 2 x 2 − x < log π 4 1
⇔ log 2 x + 2 x 2 − x > 1 ⇔ log 2 x + 2 x 2 − x > log 2 2
⇔ x + 2 x 2 − x > 2 ⇔ 2 x 2 − x > 2 − x ⇔ 2 x 2 − x > x 2 − 4 x + 4.
⇔ x 2 + 3 x − 4 > 0 ⇔ x > 1 x < − 4 .
Kết hợp điều kiện ta có T = − ∞ ; − 4 là tập nghiệm của bất phương trình.
Đáp án C
Điều kiện x ∈ ℝ .
Bất phương trình ⇔ 3. 3 x 2 − 10.3 x + 3 ≤ 0 .
⇔ 1 3 ≤ 3 x ≤ 3 ⇔ − 1 ≤ x ≤ 1
Vậy tập nghiệm của bất phương trình là T = − 1 ; 1
Suy ra a = − 1 ; b = 1 ⇒ a − b = − 2 .