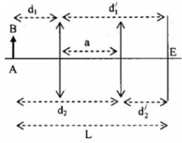
Vật phăng nhỏ AB đặt trước và song song với một màn, cách màn khoảng 100 cm. Đặt một thấu kính hội tụ giữa vật và màn, song song với vật và sao cho điểm A của vật ở trên trục chính. Ta tìm được hai vị trí của thấu kính tạo ảnh rõ nét của vật trên màn, ảnh này gấp 2,25 lần ảnh kia. Tính tiêu cự của thấu kính
A. 15 cm.
B. 40 cm.
C. 24 cm
D. 30 cm.

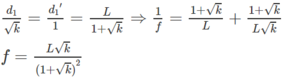
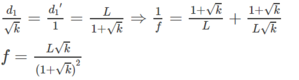
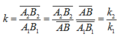 (2)
(2)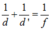
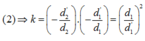 (2)
(2)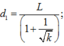
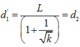
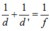
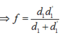
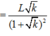
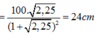
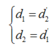
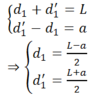
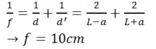
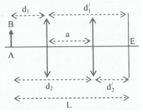

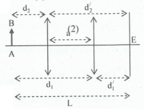

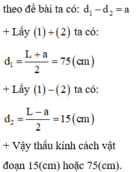


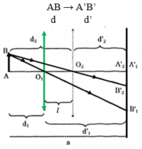
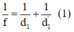
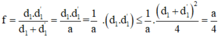

Chọn đáp án C