Có hai điện tích điểm q 1 = 10 - 8 C v à q 2 = 4 . 10 - 8 C đặt cách nhau r = 12 cm. Tính điện thế của điện trường gây ra bởi hai điện tích trên tại điểm có cường độ điện trường bằng không.
A. 6750 V
B. 6500 V
C. 7560 V
D. 6570 V
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án B
Ta có công của lực điện A = qEd.
⇒ A A ' = q q ' = 10 - 8 4 . 10 - 9 = 5 2 ⇒ A ' = 2 5 A = 24 m J

đáp án A
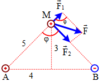
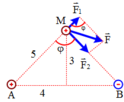
+ Các điện tích q1 và q2 tác dụng lên điện tích q các lực F1 và F2 có phương chiều như hình vẽ, có độ lớn lần lượt:
F 1 = k q 1 q r 2 = 9 . 10 9 . 10 - 8 . 10 - 8 0 , 05 2 = 3 , 6 . 10 - 4 N F 2 = k q 2 q r 2 = 9 . 10 9 . - 3 . 10 - 8 . 10 - 8 0 , 05 2 = 10 , 8 . 10 - 4 N
⇒ F = F 1 2 + F 2 2 - 2 F 1 F 2 cos φ → F = 12 , 3 . 10 - 4 N

Chọn đáp án A
A 1 = q 1 E d A 2 = q 2 E d
⇒ A 1 A 2 = q 1 q 2
hay
60 A 2 = 10 - 8 4 . 10 - 9 ⇒ A 2 = 24 m J

Đáp án A
Các điện tích q 1 và q 2 tác dụng lên điện tích q các lực F → 1 và F → 2 có phương chiều như hình vẽ, có độ lớn lần lượt:
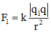
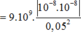
![]()
![]()
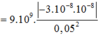
![]()
![]()
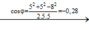
![]()

Bài làm.
Điện tích điểm q1 = 3.10-8 C đặt tại điểm A, q2 = - 4.10-8 C đặt tại điểm B, AB = 10cm.
Gọi C là điểmmà tại đó cường độ điện trường bằng không.
Gọi −−→E1CE1C→ và −−→E2CE2C→ là cường độ điện trường của q1 và q2 tại C.
Tại đó −−→E1CE1C→ = - −−→E2CE2C→. Hai vectơ này phải cùng phương, tức là điểm C phải nằm trên đường thẳng AB (Hình 3.3).
Hai vectơ này phải ngược chiều, tức là phải nằm ngoài đoan AB. Vì hai vectơ này phải có môđun bằng nhau, tức là điểm C gần A hơn B vì |q1| < |q2|.
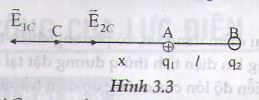
Đặt AN = l, AC = x, ta có :
k.|q1|ε.x2=k.|q2|ε.(l+x)2k.|q1|ε.x2=k.|q2|ε.(l+x)2 hay (l+xx)2=∣∣q2q1∣∣=43(l+xx)2=|q2q1|=43 hay x = 64,6cm.
Ngoài ra còn phải kể tất cả các điểm nằm rất xa q1 và q2. Tại điểm C và các điểm này thì cường độ điện trường bằng không, tức là không có điện trường
Chọn đáp án A
Muốn vậy điểm C phải nằm trên đường thẳng nối hai điện tích và trong khoảng hai điện tích.
Chọn gốc tọa độ tại A, chiều dương của trục Ox từ A đến B