Cho tứ diện đều ABCD cạnh a. Gọi M là trung điểm của BC. Tính cô-sin của góc giũa hai đường thẳng AB và DM? ...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Gọi M là trung điểm của BC. Tính cô-sin của góc giũa hai đường thẳng AB và DM?
K
Khách
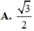
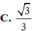
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 3 2019
Đáp án A
Giả sử tứ diện đều cạnh a
Gọi H là tâm đường tròn ngoại tiếp Δ B C D ⇒ A H ⊥ B C D
Gọi E là trung điểm
A C ⇒ M E // A B ⇒ A B , D M = M E , M D
Ta có M E = a 2 , E D = M D = a 3 2
cos
A
B
,
D
M
=
cos
M
E
,
M
D
=
cos
E
M
D
⏜
cos
E
M
D
⏜
=
M
E
2
+
M
D
2
−
E
D
2
2
M
E
.
M
D
=
3
6
21 tháng 8 2023
THAM KHẢO:
Tam giác ACD đều cạnh a có AK là trung tuyến nên AK=\(\dfrac{\sqrt{3}}{2}\)a
Gọi I là trung điểm của BD
Tam giác ABD đều cạnh a có AI là trung tuyến nên AI=\(\dfrac{\sqrt{3}}{2}\)a
Tam giác BCD có IK là đường trung bình nên IK//BC, IK=\(\dfrac{1}{2}\)BC=\(\dfrac{1}{2}\)a
Ta có: cos\(\widehat{AKI}\)=\(\dfrac{\left(\dfrac{\sqrt{3}}{2}\right)^2+\left(\dfrac{1}{2}\right)^2-\left(\dfrac{\sqrt{3}}{2}\right)^2}{2.\dfrac{\sqrt{3}}{2}.\dfrac{1}{2}}=\dfrac{\sqrt{3}}{6}\)
Nên \(\widehat{AKI}\)=\(73,2^0\)
Vì BC//IK nên góc giữa AK và BC là góc giữa AK và KI và bằng \(73,2^0\)
CM
18 tháng 2 2018
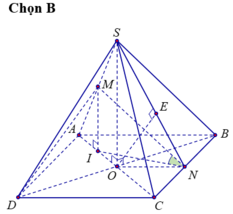
Gọi I là trung điểm OA. Vì IM// SO ⇒ IM⊥(ABCD) nên hình chiếu của MN lên (ABCD) là IN. Suy ra 
Áp dụng định lí cô sin trong ΔCIN, ta có:
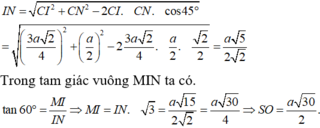
Ta có d(BC, DM) = d(BC, (SAD)) = d(N, (SAD)) = 2d(O, (SAD)) = 2d(O, (SBC)).
Kẻ OE ⊥ SN ⇒ OE ⊥ (SBC).
Ta có d(O, (SBC)) = OE mà
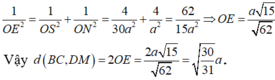
ĐÁP ÁN: B