Giải các phương trình sau, viết số gần đúng của mỗi nghiệm ở dạng số thập phân bằng cách làm tròn đến hàng phần trăm.
a) 3x – 11 = 0
b) 12 + 7x = 0
c) 10 – 4x = 2x – 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 5 2019
Đúng(0)
Những câu hỏi liên quan
0
27 tháng 3 2018
a) 3x -11 = 0 <=> 3x = 11 <=> x = \(\frac{11}{3}\)
<=> x ≈ 3, 67
Nghiệm gần đúng là x = 3,67.
b) 12 + 7x = 0 <=> 7x = -12 <=> x = \(\frac{-12}{7}\)
<=> x ≈ -1,71
Nghiệm gần đúng là x = -1,71.
c) 10 - 4x = 2x - 3 <=> -4x - 2x = -3 - 10
<=> -6x = -13 <=> x = \(\frac{13}{6}\) <=> x ≈ 2,17
Nghiệm gần đúng là x = 2, 17.
8 tháng 2 2022
a) \(3x-11=0\)
\(\Rightarrow3x=11\Rightarrow x=\dfrac{11}{3}\approx3,667\)
b) \(12+7x=0\)
\(\Rightarrow7x=-12\Rightarrow x=-\dfrac{12}{7}\approx-1,714\)
c) \(10-4x=2x-3\)
\(\Rightarrow2x+4x=10+3\Rightarrow6x=13\Rightarrow x=\dfrac{13}{6}\approx2,167\)
21 tháng 4 2017
Hướng dẫn giải:
a) 3x -11 = 0 <=> 3x = 11 <=> x = 113113
<=> x ≈ 3, 67
Nghiệm gần đúng là x = 3,67.
b) 12 + 7x = 0 <=> 7x = -12 <=> x = −127−127
<=> x ≈ -1,71
Nghiệm gần đúng là x = -1,71.
c) 10 - 4x = 2x - 3 <=> -4x - 2x = -3 - 10
<=> -6x = -13 <=> x = 136136 <=> x ≈ 2,17
Nghiệm gần đúng là x = 2, 17.
PT
21 tháng 4 2017
a) 3x -11 = 0 <=> 3x = 11 <=> x = \(\dfrac{11}{3}\)
<=> x ≈ 3, 67
Nghiệm gần đúng là x = 3,67.
b) 12 + 7x = 0 <=> 7x = -12 <=> x = \(\dfrac{-12}{7}\)
<=> x ≈ -1,71
Nghiệm gần đúng là x = -1,71.
c) 10 - 4x = 2x - 3 <=> -4x - 2x = -3 - 10
<=> -6x = -13 <=> x = \(\dfrac{13}{6}\) <=> x ≈ 2,17
Nghiệm gần đúng là x = 2, 17.
11 tháng 3 2020
\(a,3x-11=0\Leftrightarrow x=\frac{11}{3}\approx3,67\)
\(b,12+7x=0\Leftrightarrow x=-\frac{12}{7}\approx-1,71\)
\(c,10-4x=2x-3\Leftrightarrow-6x=-13\Leftrightarrow x=\frac{13}{6}\approx2,17\)
\(d,5x+3=2-x\Leftrightarrow6x=-1\Leftrightarrow x=\frac{-1}{6}\approx-0,17\)
CM
2 tháng 8 2017
3x2 – 2x = x2 + 3
⇔ 3x2 – 2x – x2 – 3 = 0
⇔ 2x2 – 2x – 3 = 0 (*)
Có a = 2; b’ = -1; c = -3; Δ’ = b’2 – ac = (-1)2 – 2.(-3) = 7 > 0
Phương trình (*) có hai nghiệm phân biệt:
JS
28 tháng 3 2020
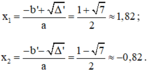
Bài 1:
a) 2(x + 1) = 3 + 2x
⇔ 2x + 2 = 3 + 2x
⇔ 0x = 1 (vô lí)
Vậy phương trình vô nghiệm.
b) 2(1 - 1,5x) + 3x = 0
⇔ 2 - 3x + 3x = 0
⇔ 2 = 0 (vô lí)
Vậy phương trình vô nghiệm.
c) |x| = - 1 (vô lí vì |x| ≥ 0)
Vậy phương trình vô nghiệm.
d) x2 + 1 = 0
⇔ x2 = -1 (vô lí vì x2 ≥ 0)
Vậy phương trình vô nghiệm.
JS
28 tháng 3 2020
Bài 2:
a) 3x - 11 = 0
⇔ 3x = 11
⇔ x = \(\frac{11}{3}\) \(\approx\) 3,67
Vậy...
b) 12 + 7x = 0
⇔ 7x = -12
⇔ x = \(\frac{-12}{7}\) \(\approx\) -1,71
Vậy...
c) 10 - 4x = 2x - 3
⇔ 6x = 13
⇔ x = \(\frac{13}{6}\approx\) 2,17
Vậy...
CM
13 tháng 5 2018
(2x - 7 )(x 10 + 3) = 0 ⇔ 2x - 7 = 0 hoặc x 10 + 3 = 0
2x - 7 = 0 ⇔ x = 7 /2 ≈ 1,323
x 10 + 3 = 0 ⇔ x = - 3/ 10 ≈ - 0,949
Phương trình có nghiệm x = 1,323 hoặc x = - 0,949