Cho tứ diện OABC có các cạnh OA, OB, OC đôi một vuông góc với nhau và OA = OB = OC = a. Khoảng cách giữa hai đường thẳng OA và BC bằng
A . 3 2 a
B . 1 2 a
C . 2 2 a
D . 3 2 a
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 4 2017
Đúng(0)
Những câu hỏi liên quan
CM
13 tháng 1 2018
Đáp án C
Phương pháp: Xác định đoạn vuông góc chung của hai đường thẳng.
Tính độ dài đoạn vuông góc chung.
Cách giải:
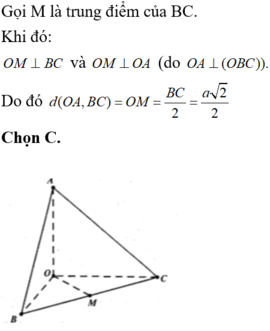
Gọi M là trung điểm của BC.
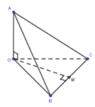
Ta có: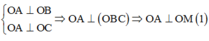 
Tam giác OBC: OB = OC => ∆OBC cân tại O, mà M là trung điểm BC 
Từ (1), (2), suy ra: OM là đoạn vuông góc chung của OA và BC => d(OA;BC) = OM
Tam giác OBC vuông tại O, OM là trung tuyến
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
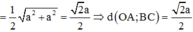
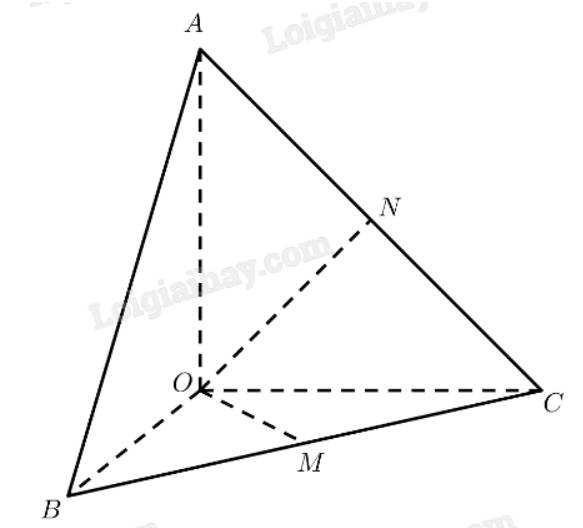
a) Gọi \(M\) là trung điểm của \(BC\).
Tam giác \(OBC\) vuông cân tại \(O \Rightarrow OM \bot BC\)
\(\left. \begin{array}{l}OA \bot OB\\OA \bot OC\end{array} \right\} \Rightarrow OA \bot \left( {OBC} \right) \Rightarrow OA \bot OM\)
\( \Rightarrow d\left( {OA,BC} \right) = OM = \frac{1}{2}BC = \frac{1}{2}\sqrt {O{B^2} + O{C^2}} = \frac{{a\sqrt 2 }}{2}\)
b) Gọi \(N\) là trung điểm của \(AC\).
Tam giác \(OAC\) vuông cân tại \(O \Rightarrow ON \bot AC\)
\(\left. \begin{array}{l}OA \bot OB\\OB \bot OC\end{array} \right\} \Rightarrow OB \bot \left( {OAC} \right) \Rightarrow OB \bot ON\)
\( \Rightarrow d\left( {OB,AC} \right) = ON = \frac{1}{2}AC = \frac{1}{2}\sqrt {O{A^2} + O{C^2}} = \frac{{a\sqrt 2 }}{2}\)
Tính khoảng cách giữa hai đường thẳng AB và OC
CM
31 tháng 8 2019
Đáp án B
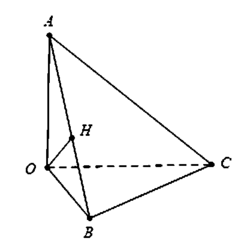
Ta có O C ⊥ O A O C ⊥ O B ⇒ O C ⊥ O A B
Kẻ O H ⊥ A B ⇒ O C ⊥ O H ⇒ d A B ; O C = O H = O A 2 = a 2 2 .