Cho hình lăng trụ đều ABCD.A'B'C'D' có đáy là hình vuông cạnh a. Mặt phẳng α lần lượt cắt các cạnh bên AA’, BB’, CC’ tại 4 điểm M, N, P, Q. Góc giữa mặt phẳng α và mặt phẳng (ABCD) là 60 0 . Diện tích tứ giác MNPQ là :
![]()
![]()
![]()
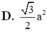
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
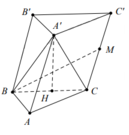
Ta có cos α = cos C C ' ; B M ^ = cos B M C ^ .
Cạnh A ' H = B C 3 2 = a 3 2 , A H = A B 3 2 = a 3 2
A A ' = A ' H 2 + A H 2 = a 6 2 ⇒ M C = a 6 4 .
Cạnh B ' H = A ' B ' 2 + A ' H 2 = a 7 2 .
Do đó cos B ' B H ^ = B B ' 2 + B H 2 - B ' H 2 2 B B ' . B H = 0 ⇒ B ' B ⊥ B H
⇒ M C ⊥ B C ⇒ c o s M B C ^ = M C B M = M C B C 2 + M C 2 = 33 11 .

Đáp án A
Thể tích của khối đa diện ABCD.MNPQ bằng thể tích khối hình hộp đứng có đáy là
ABCd và chiều cao h = 1 2 ( a 3 + 2 a 5 ) = 11 a 30
Vậy thể tích cần tính V = 11 30 a 3