Trong các hàm số dưới đây, hàm số nào chỉ có một điểm cực đại mà không có điểm cực tiểu?
A. y = − x 4 + 2 x 2 − 1
B. y = − 1 3 x 3 + x 2 − 2 x + 1
C. y = − x 4 + 2 x 2 − 1
D. y = x − 2 x + 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B

Đáp án: B.
Vì a < 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có hai cực đại, một cực tiểu.
Ở đây y' = -4 x 3 + 8x; y' = 0 ⇔ -4x( x 2 - 2) = 0
⇔ 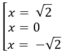

Đáp án: B.
Vì a < 0 và y' = 0 có ba nghiệm phân biệt nên hàm số y = a x 4 + b x 2 + c có hai cực đại, một cực tiểu.
Ở đây y' = -4 x 3 + 8x; y' = 0 ⇔ -4x( x 2 - 2) = 0
⇔ 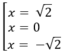

Đề đúng là \(y=mx^2+2\left(m^2-5\right)x^4+4\) chứ bạn (nghĩa là ko bị nhầm lẫn vị trí \(x^2\) và \(x^4\))
Hàm có đúng 2 điểm cực đại và 1 điểm cực tiểu khi:
\(\left\{{}\begin{matrix}2\left(m^2-5\right)< 0\\2\left(m^2-5\right).m< 0\end{matrix}\right.\)
\(\Leftrightarrow0< m< \sqrt{5}\)
\(\Rightarrow\) có 2 giá trị nguyên của m thỏa mãn

Đáp án A
Phương pháp:
Dựa vào khái niệm cực trị và các kiến thức liên quan.
Cách giải:
(1) chỉ là điều kiện cần mà không là điều kiện đủ.
VD hàm số y = x3 có y' = 3x2 = 0 ⇔ x = 0. Tuy nhiên x = 0 không là điểm cực trị của hàm số.
(2) sai, khi f''(x0) = 0, ta không có kết luận về điểm x0 có là cực trị của hàm số hay không.
(3) hiển nhiên sai.
Vậy (1), (2), (3): sai; (4): đúng

Đáp án A
Mệnh đề 1) sai vì f ' x 0 = 0 chỉ là điều kiện cần chưa là điều kiện đủ để hàm số đạt cực trị tại x 0
Mệnh đề 2) Sai vì khi f ' x 0 = f ' ' x 0 = 0 có thể hàm số có thể đạt cực trị hoặc không đạt cực trị tại x 0 .
Mệnh đề 3) sai vì f ' x đổi dấu qua điểm x 0 thì điểm x 0 có thể là điểm cực đại hoặc điểm cực tiểu của hàm số.
Mệnh đề 4) Sai vì trong trường hợp này x 0 là điểm cực tiểu của đồ thị hàm số.
Đáp án C
Hàm số:
y = − x 4 − 2 x 2 − 1 ⇒ y ' = − 4 x 3 − 4 x = 0 ⇔ x = 0
hàm số này chỉ có 1 điểm cực trị và đó là cực đại