Cho tam giác ABC trong đó BC là cạnh lớn nhất. Vì sao các góc B và C không thể là góc vuông hoặc góc tù?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a:Giả sử như \(\widehat{B}>=90^0\) thì khi đó AC là cạnh lớn nhất(trái với giả thiết)
Giả sử như \(\widehat{C}>=90^0\) thì khi đó AB là cạnh lớn nhất(Trái với giả thiết)
=>ĐPCM
b: Ta có: AB>BH
AC>CH
Do đó: AB+AC>BH+CH
=>AB+AC>BC

a)nếu góc B và góc C là góc vuông hoặc góc tù thì tương ứng sẽ là cạnh lớn nhất là AC rồi tới AB
b) ta có BH+ CH = BC mà trong 1 tam giác tổng 2 cạnh luôn luôn lớn hơn cạnh còn lại nên AB+AC > BC hay AB+AC> BH+CH

Vì góc A trong tam giác ABC là góc tù
=> Cạnh đối diện nó là cạnh lớn nhất
=> Cạnh BC lớn nhất

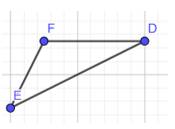
a) Vì tổng số đo 3 góc trong tam giác là 180° mà F là góc tù
\( \Rightarrow \) F > 90° do F là góc tù
\( \Rightarrow \) D + E < 180° - 90°
\( \Rightarrow \) F là góc lớn nhất trong tam giác DEF
\( \Rightarrow \) Cạnh đối diện góc F sẽ là cạnh lớn nhất tam giác DEF
\( \Rightarrow \) DE là cạnh lớn nhất
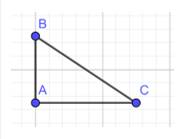
b) Tam giác ABC có góc A là góc vuông nên ta có
\( \Rightarrow \widehat B + \widehat C = {90^o} \Rightarrow \widehat B;\widehat C < {90^o}\)
\( \Rightarrow \)A là góc lớn nhất tam giác ABC
\( \Rightarrow \)BC là cạnh lớn nhất tam giác ABC do đối diện góc A

| Câu | Đúng | Sai |
| 1. Trong một tam giác vuông, cạnh đối diện với góc vuông là cạnh lớn nhất | x | |
| 2. Trong một tam giác tù, cạnh đối diện với góc tù là cạnh lớn nhất | x | |
| 3. Trong một tam giác, đối diện cạnh nhỏ nhất là góc nhọn | x | |
| 4. Trong một tam giác, đối diện với cạnh lớn nhất là góc tù | x |
*Giả sử ∠B ≥ 90o
Vì trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất nên AC > BC.
Điều này trái với giả thiết cạnh BC là cạnh lớn nhất.
*Giả sử ∠C ≥ 90o
Vì trong một tam giác cạnh đối diện với góc vuông hoặc góc tù là cạnh lớn nhất nên AB > BC.
Điều này trái với giả thiết cạnh BC là cạnh lớn nhất.
Vậy ∠B và ∠C không thể là góc vuông hoặc góc tù (là các góc nhọn).