Số tự nhiên có năm chữ số khác nhau mà tất cả các số đều là số chẵn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Các chữ só chẵn là 0; 2; 4; 8
Chữ số hàng chục nghìn có 3 lựa chọn
Chữ số hàng nghìn có 3 lựa chọn (do hàng chục nghìn- hàng lớn nhất - không thể là số 0)
Chữ số hàng trăm có 2 lựa chọn
Chữ số hàng chục có 1 lựa chọn
Chữ số hàng đơn vị có 0 lựa chọn (mâu thuẫn với đề bài)
Vậy không có số có 5 chữ số nào khác nhau mà tất cả các chữ số đều là chẵn.
Mik rất xin lỗi vì nhầm lẫn chết người khi mik để quên số 6. Mik chữa lại:
Các chữ só chẵn là 0; 2; 4; 6; 8
Chữ số hàng chục nghìn có 4 lựa chọn
Chữ số hàng nghìn có 4 lựa chọn (do hàng chục nghìn- hàng lớn nhất - không thể là số 0)
Chữ số hàng trăm có 3 lựa chọn
Chữ số hàng chục có 2 lựa chọn
Chữ số hàng đơn vị có 1 lựa chọn
Có số số hạng thỏa mãn đề bài là:
4 x 4 x 3 x 2 x 1 = 96 (số)
Đáp số: 96 số
Một lần nữa mik xin lỗi khi đã phạm lỗi nhỏ nhưng rất lớn này, mong bạn bỏ qua cho.

các số chẵn là 0,2,4,6,8 ( các số này ở hàng đơn vị của số náo thì số đó là số chẵn )



Chọn D
Không gian mẫu được mô tả là Ω : “Các số tự nhiên có 5 chữ số khác 0”.
Số phần tử của không gian mẫu là: ![]()
Gọi biến cố A: “Các số tự nhiên có 5 chữ số khác 0 trong đó chỉ có mặt ba chữ số khác nhau”.
Số cách chọn 3 chữ số phân biệt a, b, c từ 9 chữ số tự nhiên khác 0 là C 9 3 . Chọn 2 chữ số còn lại từ 3 chữ số đó, có 2 trường hợp sau:
TH1: Nếu cả 2 chữ số còn lại cùng bằng 1 trong 3 số a, b, c thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị của 5 chữ số chẳng hạn a, a, a , b, c tạo ra một số tự nhiên; nhưng cứ hoán vị của các vị trí mà a, a, a chiếm chỗ thì chỉ tạo ra cùng 1 số tự nhiên. Do đó, trong TH1 có tất cả 3 . 5 ! 5 số tự nhiên.
TH2: 1 trong 2 chữ số còn lại bằng 1 trong 3 chữ số và chữ số kia bằng một chữ số a, b, c khác trong 3 chữ số đó thì có 3 cách chọn. Mỗi hoán vị từ 5! hoán vị chẳng hạn a, a, b, b, c tạo ra một số tự nhiên nhưng cứ 2! cách hoán vị a và 2! cách hoàn vị b mà vẫn cho ra cùng 1 số. Do đó, trong TH2 có tất cả: 3 . 5 ! 2 ! . 2 ! số tự nhiên.
Suy ra số phần tử của biến cố A là: ![]()
Vậy xác suất để trong số tự nhiên được lấy ra chỉ có mặt ba chữ số khác nhau là: 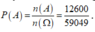

Các số có 3 chữ số khác nhau mà các chữ số đều chẵn được viết từ các chữ số:0;2;4;6;8
Ta thấy:
-Chữ số hàng trăm có 4 cách chọn.
-Chữ số hàng chục có 4 cách chọn.
-Chữ số hàng đơn vị có 3 cách chọn.
Có số số có 3 chữ số khác nhau mà các chữ số đều chẵn là:
4*4*3 = 48 (số )
Đ/s: 48 số

24680
46820