So sánh
A=10^30
B=5^30
Giải chi tiết giúp mình nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đặt d=UCLN(2n+5;3n+7)
Ta có:
2n+5chia hết cho d =>3(2n+5)=6n+15 chia hết cho d
3n+7chia hết cho d =>2(3n+7)=6n+14 chia hết cho d
=> (6n+15)-(6n+14)=1 chia hết cho d
=>d=1
vậy UCLN(2n+5;3n+7)=1 =>UC(2n+5;3n+7)=1
CHÚC BN LÀM BÀI TỐT NHÉ
2n+5 va 3n+7
=(2n+5;n+2)
=(n+3;n+2)
=(1;n+2)
Vay uc(2n+5;3n+7)=1

\(n^2+5⋮n+1\)
\(\Leftrightarrow n^2-1+6⋮n+1\)
\(\Leftrightarrow\left(n-1\right)\left(n+1\right)+6⋮n+1\)
\(\Rightarrow6⋮n+1\) \(\Rightarrow\) \(n+1\) thuộc ước của 6
=> Ư(6) = { - 6; - 3; - 2; - 1; 1; 2; 3; 6 }
=> n + 1 = { - 6; - 3; - 2; - 1; 1; 2; 3; 6 }
=> n = { - 7; - 4; - 3; - 2; 0; 1; 2; 5 }

A = \(\frac{189.123+9.4567.2+3.5310.6}{1+4+7+10+...+55+58-409}\)
A = \(\frac{189.123+18.4567+18.5310}{\left[\left(58-1\right):3+1\right].\left(58+1\right):2-409}\)
A = \(\frac{23247+18\left(4567+5310\right)}{590-409}\)
A = \(\frac{23247+177786}{181}\)
A = 201033/181
Tử số vt thừa số 9 ở 189 r
TS=18(123+4567+5310)
= 18.10000=180000
MS=1+4+7+...+58-409
=59.20:2-409
=181
A=TS/MS=180000/181
Hok tốt
Cho hình thang ABCD(AB//CD). Tìm độ dài x trong các hình vẽ bên dưới
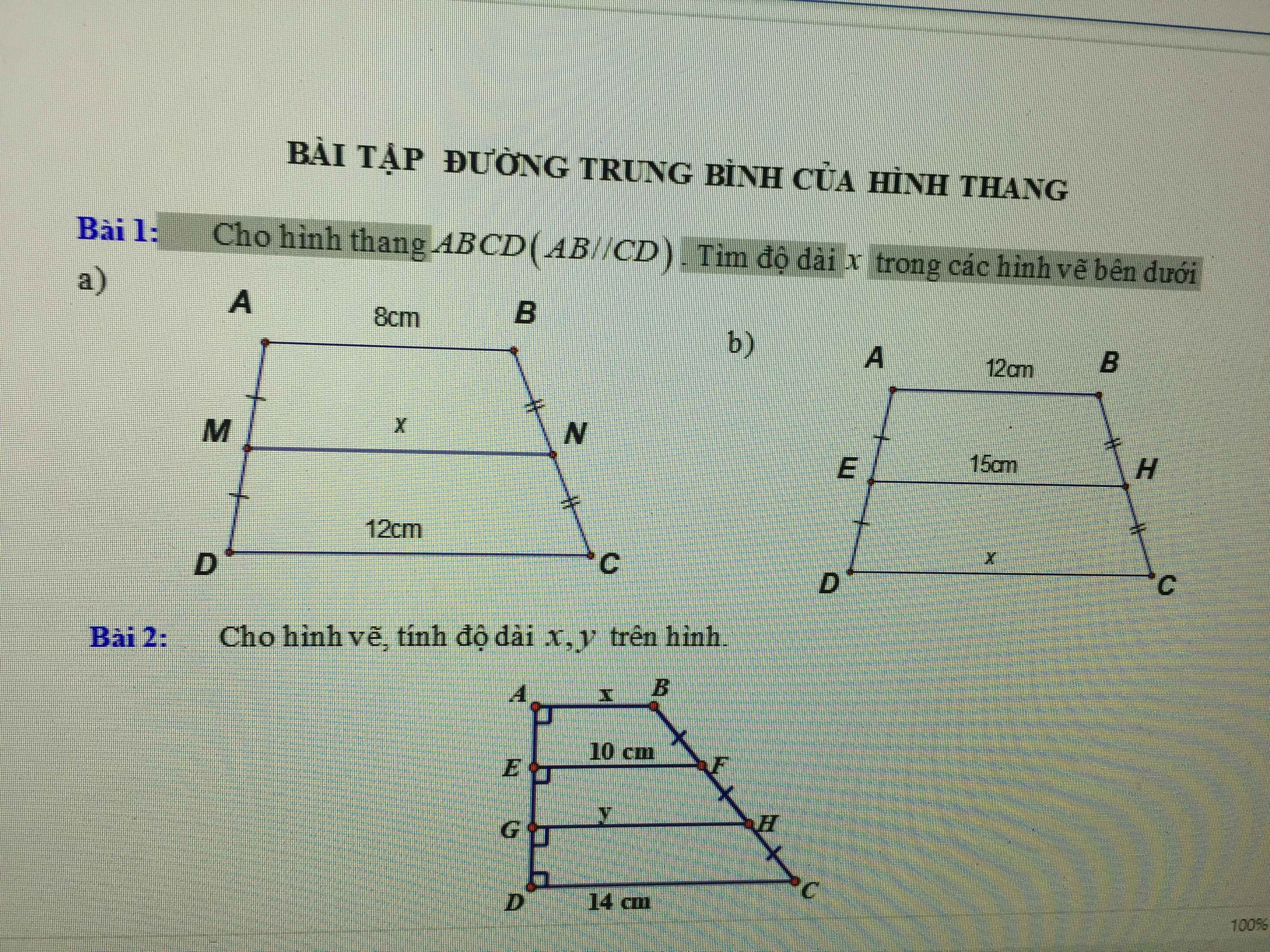
Giải chi tiết giúp mình nha


\(4,=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{5-2\sqrt{6}-9}=\dfrac{6\left(\sqrt{2}-\sqrt{3}-3\right)}{-4-2\sqrt{6}}\\ =\dfrac{3\left(3-\sqrt{2}-\sqrt{3}\right)}{2+\sqrt{6}}=\dfrac{\left(9-3\sqrt{2}-3\sqrt{3}\right)\left(\sqrt{6}-2\right)}{2}\\ =\dfrac{9\sqrt{6}-18-6\sqrt{3}+6\sqrt{2}-9\sqrt{2}+6\sqrt{3}}{2}\\ =\dfrac{9\sqrt{6}-3\sqrt{2}-18}{2}\)
\(7,=\dfrac{\sqrt{3}\left(\sqrt{3}+2\right)}{\sqrt{3}}+\dfrac{\sqrt{2}\left(\sqrt{2}+1\right)}{\sqrt{2}+1}-2-\sqrt{3}\\ =\sqrt{3}+2+\sqrt{2}+1-2-\sqrt{3}=1+\sqrt{2}\)
\(10,\dfrac{1}{\sqrt{a}+\sqrt{a+2}}=\dfrac{\sqrt{a}-\sqrt{a+2}}{a-a-2}=\dfrac{\sqrt{a-2}-\sqrt{a}}{2}\)
Do đó \(\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{5}}+...+\dfrac{1}{\sqrt{47}+\sqrt{49}}\)
\(=\dfrac{\sqrt{3}-\sqrt{1}+\sqrt{5}-\sqrt{3}+...+\sqrt{49}-\sqrt{47}}{2}=\dfrac{-1+\sqrt{49}}{2}=\dfrac{7-1}{2}=3\)
10, \(\dfrac{1}{\sqrt{1}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{5}}+...+\dfrac{1}{\sqrt{17}+\sqrt{19}}=\dfrac{\sqrt{1}-\sqrt{3}}{\left(\sqrt{1}+\sqrt{3}\right)\left(\sqrt{1}-\sqrt{3}\right)}+\dfrac{\sqrt{3}-\sqrt{5}}{\left(\sqrt{3}+\sqrt{5}\right)\left(\sqrt{3}-\sqrt{5}\right)}+...+\dfrac{\sqrt{17}-\sqrt{19}}{\left(\sqrt{17}+\sqrt{19}\right)\left(\sqrt{17}-\sqrt{19}\right)}=\dfrac{1-\sqrt{3}+\sqrt{3}-\sqrt{5}+...+\sqrt{17}-\sqrt{19}}{-2}=-\dfrac{1-\sqrt{19}}{2}\)

\(x\left(x-5\right)\left(x+5\right)-\left(x+2\right)\left(x^2-2x+4\right)=17\)
\(\Rightarrow x\left(x^2-25\right)-\left(x^3+8\right)=17\)
\(\Rightarrow x^3-25x-x^3-8=17\)
\(\Rightarrow25x=-25\Rightarrow x=-1\)

Nhận thấy 1030 và 530 đều có số mũ bằng nhau
Nhưng cơ số của 1030> cơ số của 530
=> 1030>530
=> A>B
A > B , tick nha