Tìm tất cả các giá trị của tham số m để trên đồ thị hàm số y = x 3 + 2 m − 1 x 2 + m − 1 x + m − 2 có hai điểm A, B phân biệt đối xứng nhau qua gốc tọa độ
A. 1 2 ≤ m ≤ 1
B. m > 2
C. m ∈ − ∞ ; 1 2 ∪ 1 ; + ∞
D. 1 2 < m < 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Trả lời :
Bn Do Phuong Mai đừng bình luận linh tinh nhé !
- Hok tốt !
^_^

G/s (P),(d),(d1) cùng đi qua một điểm
Gọi I(a,b) là giao điểm của (P),(d),(d1)
Có \(I\in\left(P\right),\left(d\right),\left(d1\right)\)\(\Rightarrow\left\{{}\begin{matrix}b=a^2\left(1\right)\\b=a+2\left(2\right)\\b=-a+m\left(3\right)\end{matrix}\right.\)
Từ (1);(2)\(\Rightarrow a^2=a+2\)
\(\Leftrightarrow\left[{}\begin{matrix}a=2\\a=-1\end{matrix}\right.\)
TH1: Tại \(a=2\Rightarrow b=a^2=4\)
Thay \(a=2;b=4\) vào (3) ta được:\(4=-2+m\) \(\Leftrightarrow m=6\)
TH2: Tại \(a=-1\Rightarrow b=a^2=1\)
Thay \(a=-1;b=1\) vào (3) ta được:\(1=1+m\) \(\Leftrightarrow m=0\)
Vậy m=6 hoặc m=0
Phương trình hoành độ giao điểm của (d) và (P):
\(x^2=x+2\)
\(\Leftrightarrow x^2-x-2=0\)(*)
Ta có: \(a-b+c=1-\left(-1\right)+\left(-2\right)=0\)
Do đó phương trình (*) có 2 nghiệm phân biệt
\(x_1=-1;x_2=\dfrac{-c}{a}=2\)
\(x_1=-1\) thì \(y_1=x_1^2=\left(-1\right)^2=1\)
\(x_2=2\) thì \(y_2=x_2^2=2^2=4\)
Vậy (d) và (P) cắt nhau tại 2 điểm phân biệt \(A\left(-1;1\right);B\left(2;4\right)\)
Do đó các đồ thị của (P), (d) và \(\left(d_1\right)\)cùng đi qua 1 điểm
\(\Leftrightarrow\left[{}\begin{matrix}A\in\left(d_1\right)\\B\in\left(d_1\right)\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}1=1+m\\4=-2+m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=0\\m=6\end{matrix}\right.\)
Vậy khi m=0 hoặc m=6 thì các đồ thị của (P),(d) và cùng đi qua 1 điểm
-Chúc bạn học tốt-

Chọn D.
![]() TXĐ: D = R.
TXĐ: D = R.
![]()
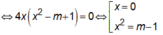
Đồ thị hàm số có 3 điểm cực trị ⇔ y' = 0 có ba nghiệm phân biệt ⇔ m -1 > 0 ⇔ m > 1(*)
3 điểm cực trị của đồ thị hàm số là: A(0;1),
Hàm số đã cho là hàm số chẵn nên đồ thị hàm số nhận Oy làm trục đối xứng
![]()
![]()
![]()
![]()
Ta có
![]()
![]()
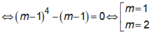
Kết hợp với điều kiện (*) => m = 2
Làm theo bào toán trắc nghiệm như sau:
Hàm số đã cho có 3 điểm cực trị khi ab < 0 ![]()
Chỉ có đáp án D thỏa mãn.

Để hai đồ thi có điểm chung thì
\(-2x^2-2x+m+3=0\) có nghiệm
\(\Leftrightarrow4-4\cdot\left(-2\right)\left(m+3\right)>=0\)
\(\Leftrightarrow4+8m+24>=0\)
hay m>=-7/4

a: Thay x=1 và y=-1 vào (d), ta được:
\(\left(m-2\right)\cdot1+m+1=-1\)
=>m-2+m+1=-1
=>2m-1=-1
=>2m=0
=>m=0
b: Thay y=0 vào y=x+2, ta được:
x+2=0
=>x=-2
Thay x=-2 và y=0 vào y=(m-2)x+m+1, ta được:
-2(m-2)+m+1=0
=>-2m+4+m+1=0
=>5-m=0
=>m=5

a) Để đồ thị hàm số \(y=\left(m-2\right)x+2\) đồng biến trên R.
=> \(m-2>0.\)
<=> \(m>2.\)
b) Đồ thị hàm số \(y=\left(m-2\right)x+2\) song song với đường thẳng \(y=5x+1.\)
=> \(m-2=5.\)
<=> \(m=7.\)
Câu 2
a) Để hs đã cho đồng biến trên R thì:
\(m-2>0\\ < =>m>2\)
b) Đề đths đã cho song song với đường thẳng \(y=5x+1\) thì:
\(m-2=5\\ < =>m=7\)
Đáp án D
Gọi A x ; y , B − x ; − y là 2 điểm đối xứng qua gốc tọa độ
Do 2 điểm thuộc đồ thị nên ta có:
y = x 3 + 2 m − 1 x 2 + m − 1 x + m − 2 − y = − x 3 + 2 m − 1 − x 2 − m − 1 x + m − 2
Cộng vế theo vế ta được:
2 m − 1 x 2 + m − 2 = 0 ⇔ x 2 = − m + 2 2 m − 1
Tồn tại 2 điểm phân biệt A, B khi x 2 > 0 , tức là − m + 2 2 m − 1 > 0 ⇔ 1 2 < m < 2