trong mặt phẳng tọa độ Oxy có các điểm M(-2;-1), N(1,5 ; 2,5), P(-0,5 ; 0;5). chứng minh 3 điểm M, N, P thẳng hàng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
30 tháng 8 2018
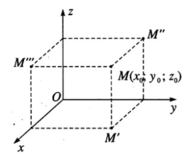
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).
Ta có:
• M’( x 0 ; y 0 ; 0)
• M’’ (0; y 0 ; z 0 )
• M’’’( x 0 ; 0; z 0 )
26 tháng 12 2021
\(\text{Đặt }M\left(x;y\right)\\ \overrightarrow{MB}\left(-2-x,2-y\right);\overrightarrow{MC}\left(-x,1-y\right)\\ \left|\overrightarrow{MB}\right|=\left|2\overrightarrow{MC}\right|\Leftrightarrow\sqrt{\left(-2-x\right)^2+\left(2-y\right)^2}=2\sqrt{\left(-x\right)^2+\left(1-y\right)^2}\\ \Leftrightarrow x^2+4x+4+y^2-4y+4=2x^2+2y^2-4y+2\\ \Leftrightarrow x^2+y^2-4y-6=0\\ \text{Mà }M\in Ox\Leftrightarrow y=0\Leftrightarrow x^2-6=0\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{6}\\x=-\sqrt{6}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}M\left(\sqrt{6};0\right)\\M\left(-\sqrt{6};0\right)\end{matrix}\right.\)
CM
12 tháng 11 2018
Do điểm M’ đối xứng với điểm M qua điểm P nên P là trung điểm MM’.
Suy ra:
x P = x M + x M ' 2 y P = y M + y M ' 2 ⇔ x M ' = 2 x P − x M = 2.9 − 0 = 18 y M ' = 2 y P − y M = 2. ( − 3 ) − 4 = − 10 ⇒ M ' ( 18 ; − 10 )
Đáp án B
CM
1 tháng 3 2018
Đáp án A
Phương trình của hai mặt phẳng (Oxy) và (Oxz) lần lượt là z = 0 và y = 0.
Điểm M(x ;y ;z) cách đều hai mặt phẳng đó khi và chỉ khi
CM
23 tháng 5 2017
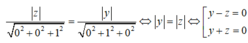
Phép vị tự tâm I(1; 2) tỉ số k = 5 biến điểm M(2; -3) thành điểm M’(x; y)
⇔ I M ' → = 5 I M → ⇔ x − 1 = 5 2 − 1 y − 2 = 5 − 3 − 2 ⇔ x = 6 y = − 23
Suy ra M’(6; -23).
Đáp án C
CM
8 tháng 8 2019
Tọa độ điểm I của đoạn thẳng MN là:
x I = x M + x N 2 = 0 + ( − 3 ) 2 = − 3 2 y I = y M + y N 2 = 4 + 2 2 = 3 ⇒ I − 3 2 ; 3
Đáp án C