Giúp mình giải bài toán hình lớp 7 này với, đây là dạng bài về Tính chất ba đường trung tuyến của tam giác
Cho 2 đoạn thẳng AB, CD cắt nhau tại trung điểm của mỗi đoạn . Gọi E , F theo thứ tự là trung điểm AD , BD . Chứng minh : CE , CF chia AB làm 3 phần bằng nhau
Gợi ý : Phải tìm ra được trọng tâm

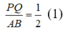 (1)
(1)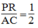 (2)
(2)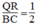
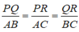
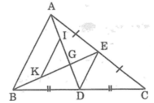
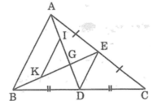
Gọi K là giao điểm AB và CD
G là giao điểm CE và AB
I là giao điểm CF và AB
Vì K là trung điểm của AB => AK = KB = 1/2 AB
Xét tam giác ACD, có:
CE là đường trung tuyến ứng với AD (E là trung điểm AD)
AK là đường trung tuyến ứng với CD ( K là trung điểm CD)
=> G là trong tâm của tam giác ACD ( giao điểm 2 đường trung tuyến)
=> GK = 1/3 AK = 1/3 BK (*)
và AG = 2/3 AK = 1/3 AB (1)
Xét tam giác BCD, có:
CF là đường trung tuyến ứng với BD (F là trung điểm BD)
BK là đường trung tuyến ứng với CD (K là trung điểm CD)
=> I là trong tâm của tam giác BCD (giao điểm 2 đường trung tuyến)
=> IK = 1/3 BK (**)
và BI = 2/3 BK = 1/3 AB (2)
Từ (*) và (**) => IK + GK = 1/3 BK + 1/3 BK = 2/3 BK = 1/3 AB (3)
Từ 1 2 và 3 => AG = GI = IB = 1/3 AB
Vậy CE và CF chia AB làm 3 đoạn bằng nhau