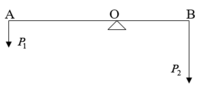
Cho hệ thống như hình 79. Thanh AC đồng chất có trọng lượng 3N, đầu A treo vật có trọng lượng 4N.
a) Tìm trọng lượng phải treo tại B để cho hệ cân bằng.
b) Nếu treo vào đầu C một vật có khối lượng m thì m phải bằng bao nhiêu để thanh cân bằng.

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Quy tắc momen ngẫu lực:
\(M_A=M_B\Rightarrow OA\cdot F_A=OB\cdot F_B\)
\(\Rightarrow2OB\cdot m_1=OB\cdot m_2\Rightarrow2m_1=m_2\)
\(\Rightarrow m_2=2\cdot8=16kg\)
Vậy phải treo ở đầu B vật có khối lượng 16kg để thanh AB cân bằng.

Đáp án C
- Vì thanh nhẹ có thể quay quanh điểm O nên ta coi O là điểm tựa của đòn bẩy.
- Để hệ thống cân bằng ta có điều kiện cân bằng đòn bẩy như sau:
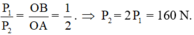
- Khối lượng vậy treo vào đầu B là:
160 : 10 = 16 (kg)

a/ Tổng tất cả các lực t/d= 100+300=400(N)
b/ Khối lượng của thanh sẽ t/d lên trung điểm của thanh, ta nhận thấy Pa<Pb \(\Rightarrow P_A.d_A+P.d=P_B.d_B\Leftrightarrow100.\left(\dfrac{AB}{2}+d\right)+5000.d=300.\left(\dfrac{AB}{2}-d\right)\)
(d là khoảng cách giữa trọng tâm thanh đến điểm tựa)
Từ đó bạn tìm được d

gọi l1 là chiều dài cánh tay đòn 1 ( ở đây là OA) l2 là chiều dài cánh tay đòn 2 ( ở đây là OB)
l1+l2=150 cm =1,5 m (1)
m1=3kg => P1=30(N)
m2=6kg => P2=60(N)
Để hệ thống cân bằng thì:
m1.l1=m2.l2
=> 30l1=60l2 => l1 - 2l2= 0 ( đơn giản mỗi vế cho 30) (2)
Từ (1) và (2) ta có hệ phương trình
l1+l2=1,5
l1 - 2l2=0
=> l1=1 (m)
l2=0,5(m)