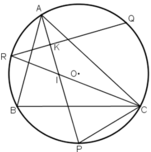
Cho tam giác ABC nội tiếp đường tròn. P,Q,R theo thứ tự là các điểm chính giữa của các cung bị chắn BC, CA, AB bởi các góc A, B, C.
AP cắt CR tại I. Chứng minh tam giác CPI là tam giác cân.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
21 tháng 11 2019
a) Gọi K là giao điểm của QR và AP.
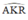là góc có đỉnh K nằm bên trong đường tròn
⇒ AP ⊥ QR.
+ R, P lần lượt là điểm chính giữa các cung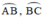 
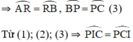
⇒ ΔPCI cân tại P.
Kiến thức áp dụng
+ Số đo của góc có đỉnh nằm bên trong đường tròn bằng nửa tổng số đo hai cung bị chắn.
+ Số đo của góc nội tiếp bằng một nửa số đo cung bị chắn.
LH
11 tháng 4 2017
a) Gọi giao điểm của AP và QR là K.
\(\widehat{AKR}\) là góc có đỉnh ở bên trong đường tròn nên
\(\widehat{AKR}\) = sđcung(AR +QC + CP)/2 =
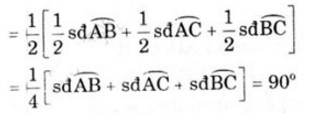
Vậy \(\widehat{AKR}\) = 900 hay AP \(\perp\) QR
b) \(\widehat{CIP}\) là góc có đỉnh ở bên trong đường tròn nên:
\(\widehat{CIP}\) = sđcung(AR +CP)/2 (1)
\(\widehat{PIC}\) góc nội tiếp, nên \(\widehat{PIC}\)= (sđ cung RB + BP)/2 (2)
Theo giả thiết thì cung AR = RB (3)
Cung CP = BP (4)
Từ (1), (2), (3), (4) suy ra: \(\widehat{CIP}\) = \(\widehat{PIC}\). Do đó \(\Delta\)CPI cân.
CM
11 tháng 1 2017
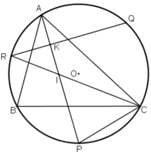
Gọi K là giao điểm của QR và AP.
là góc có đỉnh K nằm bên trong đường tròn
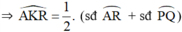
⇒ AP ⊥ QR.
20 tháng 3 2023
a: góc RQP+góc QPA
=1/2*(sđ cung RP+sđ cung QA)
=1/2*(1/2*sđ cung CA+1/2sđcung AB+1/2sđcungBC)
=1/4*360=90 độ
=>AP vuông góc QR
b: góc CIP=1/2(sđ cung CP+sđ cung AR)
=1/2(sđ cung BP+sđcung RB)
=1/2*sd cung PR
=góc ICP
=>ΔCPI cân tại P
+ R, P lần lượt là điểm chính giữa các cung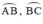
⇒ ΔPCI cân tại P.