Một ôtô có khối lượng m = 2,5 tấn rời khỏi bến. Lực phát động bằng 2500N. Hệ số ma sát lăn giữa bánh xe với mặt đường là μ = 0 , 08 . Hỏi sau khi chuyển bánh được 2 phút thì ôtô đạt được vận tốc là bao nhiêu và đã đi được quãng đường bao nhiêu? Lấy g = 9 , 8 m / s 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khi ôtô chuyển động thẳng đều, lực phát động cân bằng với lực ma sát lăn. Về độ lớn:
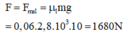

a/ (0,5 điểm) 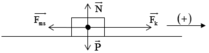
b/ (0,5 điểm)
Gia tốc: 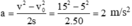
c/ (1,0 điểm)
Áp dụng định luật II Niu – tơn: 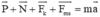
Chiếu lên chiều dương (hoặc chiếu lên chiều chuyển động)
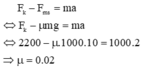

Trọng lượng của ôtô con bằng đúng áp lực của nó tác dụng xuống mặt đường:
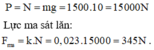

Đổi : 4 tấn =4000 kg; 18 km/h=5m/s; 54km/h=15 m/s ; 72 km/h=20m/s
Gia tốc của ô tô đó
\(a=\dfrac{v^2-v_0^2}{2s}=\dfrac{15^2-5^2}{2\cdot50}=2\left(\dfrac{m}{s^2}\right)\)
Theo định luật Niu-tơn II
\(N+F_k+F_{ms}+P=m\cdot a\)
Chiếu theo Oy: N =P = mg=4000.10=40000(N)
Chiếu theo Ox:\(F_k-F_{ms}=m\cdot a\Rightarrow F_k=m\cdot a+\mu\cdot N=4000\cdot2+0,05\cdot40000=10000\left(N\right)\)
Thời gian từ lúc tăng tốc đến lúc đạt vận tốc 72 km/h
\(t=\dfrac{v'-v_0}{a}=\dfrac{20-5}{2}=7,5\left(s\right)\)
Quãng đường đi được trong thời gian đó
\(s=\dfrac{v'^2-v_0^2}{2a}=\dfrac{20^2-5^2}{2\cdot2}=93,75\left(m\right)\)

Vật chuyển động đều trên đường nằm ngang.
\(\Rightarrow\overrightarrow{F}+\overrightarrow{F_{ms}}=\overrightarrow{0}\)
\(\Rightarrow F-F_{ms}=0\)
\(\Rightarrow F=F_{ms}=\mu mg=0,2\cdot2000\cdot10=4000N\)
Công của lực kéo và lực ma sát lúc này bằng nhau.
\(\Rightarrow A_{F_k}=A_{ms}=F\cdot s=4000\cdot250=10^6J\)

Từ kết quả lí thuyết, ta có biểu thức gia tốc