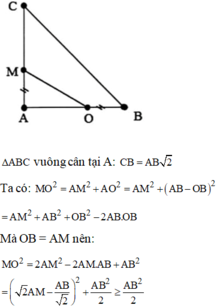
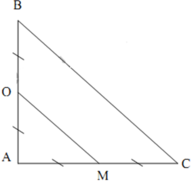
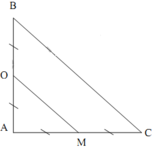
Cho tam giác ABC vuông cân tại A nằm trong một môi trường truyền âm. Một nguồn âm điểm O có công suất không đổi phát âm đẳng hướng đặt tại điểm B khi đó một người M đứng lại C nghe được âm có mức cường độ âm là 40dB. Sau đó di chuyển nguồn âm O trên đoạn AB và người M di chuyển trên đoạn AC sao cho BO = AM. Mức cường độ âm lớn nhất mà người đó nghe được trong quá trình cả hai di chuyển bằng
A.56,6dB.
B.46,0dB.
C. 42,0dB.
D. 60,2dB.


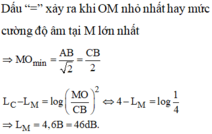
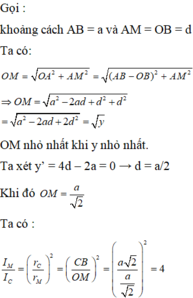
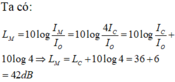
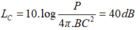
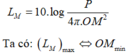


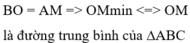
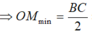
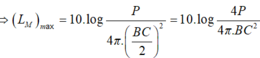
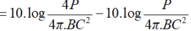
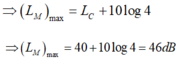
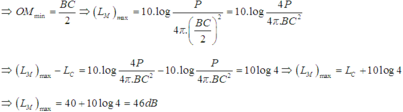

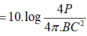
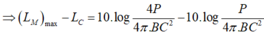

Chọn B.
Δ A B C vuông cân tại A: C B = A B 2
Ta có: M O 2 = A M 2 + A O 2 = A M 2 + A B − O B 2
= A M 2 + A B 2 + O B 2 − 2 A B . O B
Mà OB = AM nên:
M O 2 = 2 A M 2 − 2 A M . A B + A B 2 = 2 A M − A B 2 2 + A B 2 2 ≥ A B 2 2
Dấu “=” xảy ra khi OM nhỏ nhất hay mức cường độ âm tại M lớn nhất
⇒ M O min = A B 2 = C B 2
L − C L M = log M O C B 2 ⇔ 4 − L M = log 1 4 ⇒ L M = 4,6 B = 46 d B .