Tính diện tích mặt cầu ngoại tiếp một hình chóp tứ giác đều có cạnh bên bằng 2 và cạnh đáy bằng 1
A. 32 π 7
B. 8 π 7
C. 128 π 21 14
D. 16 π 14
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
3 tháng 12 2018
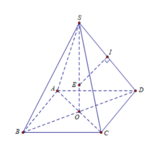
Đáp án A
Áp dụng công thức giải nhanh ta có R = S A 2 2 S O
Trong đó S A = 2 ; O A = 1 2 ; S O = 4 − 1 2 = 14 2
Do đó R = 4 14
VẬY diện tích mặt cầu ngoại tiếp một hình chóp là: s = 4 π R = 4 π 4 14 = 32 π 7
CM
25 tháng 10 2018
Đáp án A
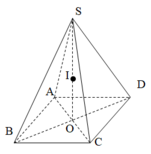
Gọi I là tâm mặt cầu ngoại tiếp hình chóp tứ giác đều
CM
10 tháng 9 2018
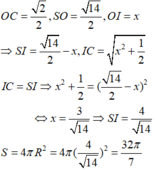
Gọi O là tâm hình vuông của mặt đáy. Khi đó O cũng là tâm của mặt cầu. Ta có:
R 2 = S O 2 = a 2 - a 2 2 2 = a 2 2 S = 4 πR 2 = 2 πa 2
Đáp án C
NV
Nguyễn Việt Lâm
Giáo viên
24 tháng 8 2021
Gọi O là tâm đáy \(\Rightarrow AO=\dfrac{a\sqrt{3}}{3}\)
\(SA=\dfrac{AO}{cos60^0}=\dfrac{2a\sqrt{3}}{3}\)
\(SO=\sqrt{SA^2-AO^2}=a\)
\(\Rightarrow R=\dfrac{SA^2}{2SO}=\dfrac{2a}{3}\)
\(V=\dfrac{4}{3}\pi R^3=\dfrac{32\pi a^3}{81}\)
\(\Rightarrow\dfrac{V}{\pi a^3}=\dfrac{32}{81}\)
Đáp án A