Cho hàm số y = f x có đạo hàm f ' x = x − 1 2 x 2 − 2 x , với mọi x ∈ ℝ . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số y = f x 2 − 8 x + m có 5 điểm cực trị?
A. 16
B. 17
C. 15
D. 18
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
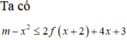
![]()
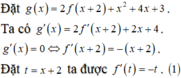
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
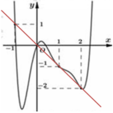
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có




Đáp án D.
Ta có thể lập bảng xét dấu của f'(x) tuy nhiên thì ta có thể dùng mẹo như sau. Tại x=0; x=-2 thì y' đổi dấu do có mũ la lẻ còn x=1 thì không đổi dấu do mũ là chẵn. Vì vậy ta có thể có 2 cực trị.

Ta có:
f ' ( x ) = x ( x + 1 ) ( x - 2 ) 2 = 0 ⇔ [ x = 0 x = - 1 x = 2
với x=2 là nghiệm kép.
Ta có bảng biến thiên như sau:
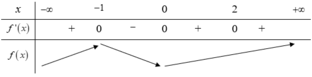
Dựa vào bảng biến thiên ta thấy hàm số đạt giá trị nhỏ nhất trên đoạn [-1;2] tại x=0.
Chọn đáp án B.
Đáp án C.
Ta có:
g ' x = 2 x − 8 f ' x 2 − 8 x + m = 0 ⇔ x = 4 f ' x 2 − 8 x + m = 0 ( * ) .
Mà:
f ' x = x − 1 2 x 2 − 2 x = x − 1 2 . x x − 2 ; ∀ x ∈ ℝ .
Suy ra (*)
⇔ x 2 − 8 x + m − 1 2 x 2 − 8 x + m x 2 − 8 x + m − 2 = 0 ⇔ x 2 − 8 x + m − 1 = 0 1 x 2 − 8 x + m = 0 2 x 2 − 8 x + m − 2 = 0 3
Để hàm số đã cho có 5 điểm cực trị khi và chỉ khi:
TH1. (1) có nghiệm kép x = 4 , (2), (3) có 2 nghiệm phân biệt.
TH2. (1) không có nghiệm kép x = 4 , (2), (3) có 2 nghiệm phân biệt.
Khi đó m < 16 là các giá trị thỏa mãn. Kết hợp m ∈ ℤ + ⇒ có 15 giá trị m cần tìm.