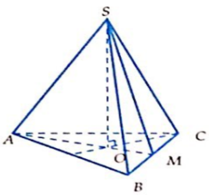
Cho hình chóp tam giác đều đáy có cạnh bằng a, góc tạo bởi các mặt bên và đáy bằng 60°. Thể tích khối chóp là:
A. V = a 3 3 24
B. V = a 3 6 24
C. V = a 3 3 8
D. V = a 3 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\)
Gọi M là trung điểm AB \(\Rightarrow AB\perp OM\Rightarrow AB\perp\left(SOM\right)\)
\(\Rightarrow\widehat{SMO}\) là góc giữa mặt bên và đáy hay \(\widehat{SMO}=60^0\)
\(SO=OM.tan\widehat{SMO}=\dfrac{a}{2}.tan60^0=\dfrac{a\sqrt{3}}{2}\)
\(V=\dfrac{1}{3}SO.S_{ABCD}=\dfrac{1}{3}.\dfrac{a\sqrt{3}}{2}.a^2=\dfrac{a^3\sqrt{3}}{6}\)

Đáp án C
Phương pháp:
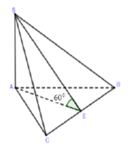
- Xác định góc giữa hai mặt phẳng S.ABC bởi định nghĩa:
Góc giữa hai mặt phẳng là góc giữa hai đường thẳng nằm trong hai mặt phẳng mà cùng vuông góc với giao tuyến.
- Tính thể tích khối chóp theo công thức
V = 1 3 S h


Chọn B
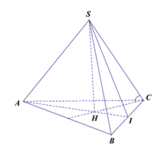
Gọi H là trọng tâm tam giác ABC, khi đó
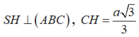
Góc giữa cạnh bên và mặt đáy là góc
![]()


Đáp án A
Gọi H là hình chiếu của S lên lên (ABCD).

A H = 2 3 a 2 - a 2 2 = a 3 3 S H = A H tan 60 ∘ = a 3 3 . 3 = a
Thể tích khối chóp là:
V = 1 3 S A B C · S H = 1 3 · 1 2 a 2 sin 60 ° . a = a 3 . 3 12

Đáp án D
Gọi d là tiếp tuyến của (C) tại điểm A(1:0).
Ta có: y ' = 3 x 2 − 6 x ⇒ y ' 1 = 3.
Suy ra: d : − 3 x − 1 + 0 ⇔ y = − 3 x + 3.

Đáp án D
Gọi H là tâm của tam giác ABC. Trong (SBC), kẻ SI vuông góc BC.
Do góc giữa mặt bên và mặt đáy là 600 suy ra
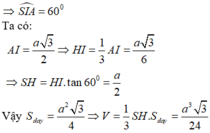
Đáp án A