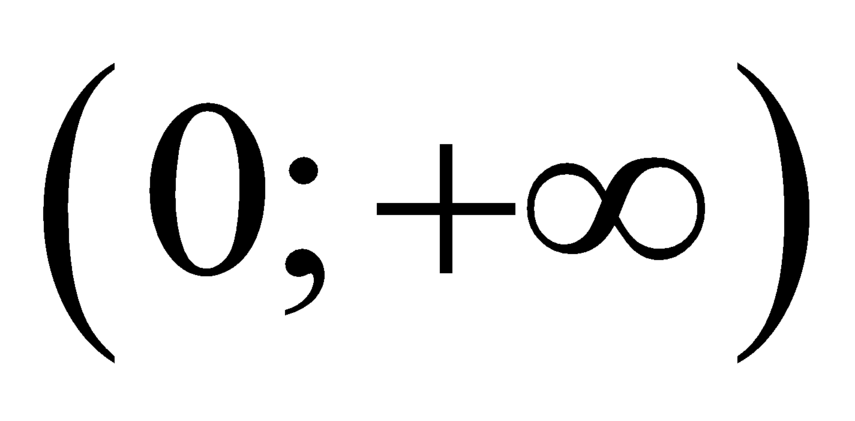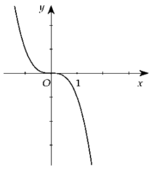
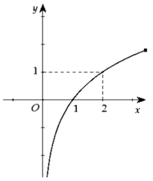
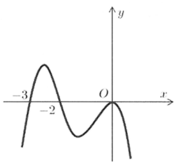
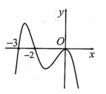
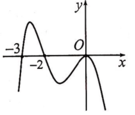
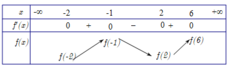
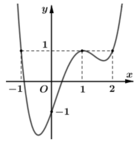
Cho hàm số y= f(x) liên tục và xác định trên R. Biết f( x) có đạo hàm f’( x) và hàm số y= f’( x) có đồ thị như hình vẽ, khẳng định nào sau đây đúng?
A. Hàm số y= f( x) đồng biến trên R
B. Hàm số y= f( x) nghịch biến trên R.
C. Hàm số y= f( x) chỉ nghịch biến trên khoảng ![]() .
.
D. Hàm số y= f( x) nghịch biến trên khoảng (0; + ∞) .

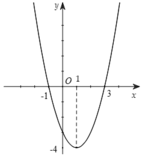


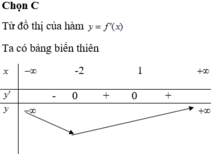

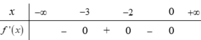

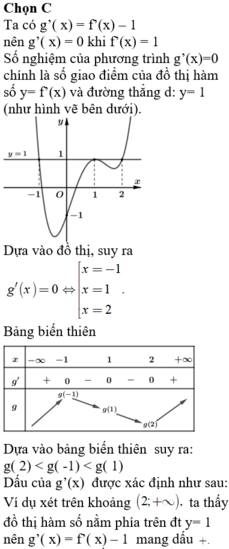
Chọn D
Trong khoảng (0 ; + ∞) đồ thị hàm số y= f’( x) nằm phía dưới trục hoành- tức là f’( x)< 0 trên khoảng đó
=> Hàm số y= f(x) nghịch biến trên khoảng