Chứng minh đẳng thức: u − uv + v − v 2 v 3 − 3 v 2 + 3 v − 1 = u + v − v 2 + 2 v − 1 với v ≠ 1 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TT
1
4 tháng 11 2017
Ta có :
<=> u3 - 3u - 2 \(\le\) v3 - 3v + 2 <=> ( u + 1 )2( u - 2 ) \(\le\) ( v - 1 )2( v + 2 )
Đặt x = u + 1 , y = v -1 thì :
BĐT <=> x3 - 3x2 \(\le\) y3 + 3y2 <=> x3 - y3 \(\le\) 3(x2 + y2)
Ta có : x - y = ( u - v ) + 2 \(\le\)2
=> ( x - y ) ( x2 + xy + y2 ) \(\le\)2( x2 + xy + y2) = 2(x2 + y2) + 2xy \(\le\) 2(x2 + y2) + ( x2 + y2 ) = 3(x2 + y2 ) => x3 - y3 \(\le\) 3(x2 +y2 ) ( đpcm)
Dấu bằng xảy ra khi <=> x = y = 0 <=> u = -1 ; v = 1
30 tháng 7 2018
u^2v^2(u+v)^2-(u^2v+uv^2)^2 - Step-by-Step Calculator - Symbolab
Tham khảo ở đó nhé!
TM
19 tháng 5 2016
\(\frac{u+2}{u-2}=\frac{v+3}{v-3}\)
\(\Rightarrow\left(u+2\right).\left(v-3\right)=\left(u-2\right).\left(v+3\right)\)
\(\Rightarrow u\left(v-3\right)+2\left(v-3\right)=u\left(v+3\right)-2\left(v+3\right)\)
\(\Rightarrow uv-3u+2v-6=uv+3u-2v-6\Rightarrow uv-3u+2v=uv+3u-2v\)
\(\Rightarrow-3u+2v=3u-2v\Rightarrow2v-3u=3u-2v\Rightarrow2v+2v=3u+3u\Rightarrow4v=6u\Rightarrow\frac{u}{3}=\frac{v}{2}\)
29 tháng 8 2020
Bài 1:
a) Ta có: \(VT=\frac{-u^2+3u-2}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(u^2-3u+2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(n^2-u-2u+2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left[u\left(u-1\right)-2\left(u-1\right)\right]}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{-\left(u-1\right)\left(u-2\right)}{\left(u+2\right)\left(u-1\right)}\)
\(=\frac{2-u}{u+2}\)(1)
Ta có: \(VP=\frac{u^2-4u+4}{4-u^2}\)
\(=\frac{\left(u-2\right)^2}{-\left(u-2\right)\left(u+2\right)}\)
\(=\frac{-\left(u-2\right)}{u+2}\)
\(=\frac{2-u}{u+2}\)(2)
Từ (1) và (2) suy ra \(\frac{-u^2+3u-2}{\left(u+2\right)\left(u-1\right)}=\frac{u^2-4u+4}{4-u^2}\)
b) Ta có: \(VT=\frac{v^3+27}{v^2-3v+9}\)
\(=\frac{\left(v+3\right)\left(v^3-3u+9\right)}{v^2-3u+9}\)
\(=v+3=VP\)(đpcm)
Bài 2:
a) Ta có: \(\frac{3x^2-2x-5}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{3x^2-5x+3x-5}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{x\left(3x-5\right)+\left(3x-5\right)}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow\frac{\left(3x-5\right)\left(x+1\right)}{M}=\frac{3x-5}{2x-3}\)
\(\Leftrightarrow M=\frac{\left(3x-5\right)\left(x+1\right)\left(2x-3\right)}{3x-5}\)
\(\Leftrightarrow M=\left(x+1\right)\left(2x-3\right)\)
\(\Leftrightarrow M=2x^2-3x+2x-3\)
hay \(M=2x^2-x-3\)
Vậy: \(M=2x^2-x-3\)
b) Ta có: \(\frac{2x^2+3x-2}{x^2-4}=\frac{M}{x^2-4x+4}\)
\(\Leftrightarrow\frac{2x^2+4x-x-2}{\left(x-2\right)\left(x+2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{2x\left(x+2\right)-\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{\left(x+2\right)\left(2x-1\right)}{\left(x+2\right)\left(x-2\right)}=\frac{M}{\left(x-2\right)^2}\)
\(\Leftrightarrow\frac{M}{\left(x-2\right)^2}=\frac{2x-1}{x-2}\)
\(\Leftrightarrow M=\frac{\left(2x-1\right)\left(x-2\right)^2}{\left(x-2\right)}\)
\(\Leftrightarrow M=\left(2x-1\right)\left(x-2\right)\)
\(\Leftrightarrow M=2x^2-4x-x+2\)
hay \(M=2x^2-5x+2\)
Vậy: \(M=2x^2-5x+2\)
Bài 3:
a) Ta có: \(\frac{x+1}{N}=\frac{x^2-2x+4}{x^3+8}\)
\(\Leftrightarrow\frac{x+1}{N}=\frac{x^2-2x+4}{\left(x+2\right)\left(x^2-2x+4\right)}\)
\(\Leftrightarrow\frac{x+1}{N}=\frac{1}{x+2}\)
\(\Leftrightarrow N=\left(x+1\right)\left(x+2\right)\)
hay \(N=x^2+3x+2\)
Vậy: \(N=x^2+3x+2\)
n) Ta có: \(\frac{\left(x-3\right)\cdot N}{3+x}=\frac{2x^3-8x^2-6x+36}{2+x}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=\frac{2x^3+4x^2-12x^2-24x+18x+36}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{\left(x+3\right)}=\frac{2x^2\left(x+2\right)-12x\left(x+2\right)+18\left(x+2\right)}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=\frac{\left(x+2\right)\left(2x^2-12x+18\right)}{x+2}\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=2x^2-12x+18\)
\(\Leftrightarrow\frac{N\cdot\left(x-3\right)}{x+3}=2x^2-6x-6x+18=2x\left(x-3\right)-6\left(x-3\right)=2\cdot\left(x-3\right)^2\)
\(\Leftrightarrow N\cdot\left(x-3\right)=\frac{2\left(x-3\right)^2}{x+3}\)
\(\Leftrightarrow N=\frac{2\left(x-3\right)^2}{x+3}:\left(x-3\right)=\frac{2\left(x-3\right)^2}{\left(x+3\right)\left(x-3\right)}\)
\(\Leftrightarrow N=\frac{2\left(x-3\right)}{x+3}\)
hay \(N=\frac{2x-6}{x+3}\)
Vậy: \(N=\frac{2x-6}{x+3}\)
11 tháng 8 2020
mình có sửa lại đề 1 chút!
đặt \(T=\sqrt{\frac{u-8\sqrt[6]{u^3v^2}+4\sqrt[3]{v^2}}{\sqrt{u}-2\sqrt[3]{v}+2\sqrt[12]{u^3v^2}}+3\sqrt[3]{v}}+\sqrt[6]{v}=1\)
đặt \(u=a^4;v=b^6\)(a,b>0) ta có
\(T=\frac{u-8\sqrt[6]{u^3v^2}+4\sqrt[3]{v^2}}{\sqrt{u}-2\sqrt[3]{v}+2\sqrt[12]{u^3v^2}}+3\sqrt[3]{v}=\frac{a^4-8a^2b^2+4b^2}{a^2-2b^2+2ab}+3b^2\)
vậy \(T=\frac{a^4-8a^2b^2+4b^4}{a^2-2b^2+2ab}+3b^2=\frac{a^4-5a^2b^2-2b^4+6ab^3}{a^2-2b^2+2ab}=a^2-2ab+b^2\)
từ đó suy ra \(\sqrt{\frac{u-8\sqrt[6]{u^3v^2}+4\sqrt[3]{v^2}}{\sqrt{u}-2\sqrt[3]{v}+2\sqrt[12]{u^3v^2}}+3\sqrt[3]{v}}+\sqrt[6]{v}=\left|\sqrt[4]{u}-\sqrt[6]{v}\right|+\sqrt[6]{v}\)
vì \(u^3\ge v^2\)nên \(\left|\sqrt[4]{u}-\sqrt[6]{v}\right|+\sqrt[6]{v}=\sqrt[4]{u}\)
\(\sqrt{\frac{u-8\sqrt[6]{u^3v^2}+4\sqrt[3]{v^2}}{\sqrt{u}-2\sqrt[3]{v}+2\sqrt[12]{u^3v^2}}+3\sqrt[3]{v}}+\sqrt[6]{v}=1\)
với u=1 ta có \(T=\sqrt{\frac{1-8\sqrt[6]{v^2}+4\sqrt[3]{v^2}}{1-2\sqrt[3]{v}+2\sqrt[6]{v^2}}+3\sqrt[3]{v}}+\sqrt[6]{v}\)
nếu \(1-2\sqrt[3]{v}+2\sqrt[6]{v}=0\)thì \(\sqrt[3]{v}=\frac{3+1}{2}>0\)
do \(v^2>1=u^3\), mâu thuẫn suy ra \(1-2\sqrt[3]{v}+2\sqrt[6]{v}\ne0\)
tóm lại với \(u^3\ge v^2\)và u,v\(\inℚ^+\)để \(\sqrt{\frac{u-8\sqrt[6]{u^3v^2}+4\sqrt[3]{v^2}}{\sqrt{u}-2\sqrt[3]{v}+2\sqrt[12]{u^3v^2}}+3\sqrt[3]{v}}+\sqrt[6]{v}=1\)cần và đủ là u=1 và v<1, v\(\inℚ^+\)được lấy tùy ý
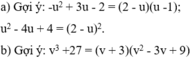
Gợi ý: u – uv + v – v 2 = (1 – v)(u + z).