Cho hình lăng trụ đứng ABC. A’B’C’ có đáy là tam giác vuông cân tại đỉnh A, mặt bên BCC’B’ là hình vuông, khoảng cách giữa AB’ và CC’ bằng a. Thể tích của khối trụ ABC. A’B’C’.
A. a 3
B. 2 a 3 2
C. 2 a 3 3
D. 2 a 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Hướng dẫn giải:
Ta có C'C//(ABB'A')
![]()
Lại có C ' A ' ⊥ B B ' , C ' A ' ⊥ A ' B '
![]()
Khi đó B ' C ' = a 2
Mà BCC’B’ là hình vuông nên chiều cao của hình lăng trụ
Kết luận
V A B C . A ' B ' C ' = 1 2 a 2 . a 2 = a 2 3 2

Đáp án là B
Ta có d ( A B ' ; C C ' ) = d ( C ; ( A B B ' A ' ) ) = C A = a
B C = a 2 ⇒ V = a 2 . 1 2 a 2 = a 2 2 2

Chọn đáp án D
Gọi M là trung điểm của BC. Suy ra
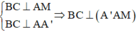
![]()
![]()
![]()
Ta có
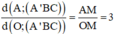
![]()
∆ A ' A M vuông tại A, AH là đường cao nên
![]()
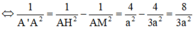
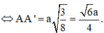
Thể tích khối lăng trụ là: V A B C . A ' B ' C ' = 3 2 a 3 16