Cho hình vuông ABCD, điểm E thuộc cạnh CD. Tia phân giác của góc ABE cắt AD ở K. Chứng minh AK + CE = BE.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
1 tháng 6 2019
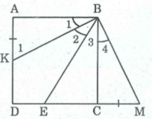
Trên tia đối của tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (1)
Xét ∆ ABK và ∆ CBM, ta có:
AB = CB (gt)
∠ A = ∠ C = 90 0
AK = CM (theo cách vẽ)
Suy ra: ∆ ABK = ∆ CBM (c.g.c)
⇒ ∠ B 1 = ∠ B 4 (2)
Lại có: ∠ B 1 = ∠ B 2 ( do BK là tia phân giác của ABE)
Suy ra: ∠ B 1 = ∠ B 2 = ∠ B 4
Mà ∠ (KBC) = 90 0 - ∠ B 1 (3)
Tam giác CBM vuông tại C nên: ∠ M = 90 0 - ∠ B 4 (4)
Từ (2), (3) và (4) suy ra: ∠ (KBC) = ∠ M (5)
Hay ∠ B 2 + ∠ B 3 = ∠ M
⇒ ∠ B 4 + ∠ B 3 = ∠ M( vì ∠ B 2 = ∠ B 4 )
Hay: ∠ (EBM) = ∠ M
⇒ ∆ EBM cân tại E ⇒ EM = BE. (6)
Từ (1) và (6) suy ra: AK + CE = BE.
2 tháng 10 2016
trên tia đối của AD lấy N sao cho AN = CE
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE
8 tháng 12 2018
trên tia đối của AD lấy N sao cho AN = CE
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE
6 tháng 8 2015
ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE^ = ABN^ (1)
BK là phân giác của ABE^ nên:
KBE^ = KBA^ (2)
(1) + (2) được:
CBE^ + KBE^ = ABN^ + KBA^
=> CBK^ = KBN^ (*)
mà: CBK^ = BKN^ (**) ( so le trong)
(*) và (**) => BKN^ = KBN^ => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(3) và (4) => CE + AK = BE
~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
li-ke cho minhf nhes bn Nguyễn Thị Thùy Trang
ND
1
LN
7 tháng 1 2017
Trên tia đối của AD lấy N sao cho AN = CE
Ta có:
Δ BCE = Δ BAN (2 cạnh góc vuông = nhau)
=> CBE= ABN (1)
BK là phân giác của ABE nên:
KBE = KBA (2)
(1) + (2) được:
CBE + KBE = ABN + KBA
=> CBK = KBN(3)
mà: CBK= BKN(4) ( so le trong)
(3) và (4) => BKN = KBN => BNK là tam giác cân tại N
=> NB = NK
=> NB = AN + AK = CE + AK (3)
do: Δ BCE = Δ BAN => BE = NB (4)
(5) và (6) => CE + AK = BE
5 tháng 6 2019
Trên tia đối của tia AD lấy điểm F sao cho AF =EC
Chứng minh đc: \(\Delta ABF=\Delta CBE\)( cạnh góc vuông-cạnh góc vuông)
=> \(\widehat{ABF}=\widehat{CBE}\)
mà \(\widehat{EBK}=\widehat{KBA}\)
=> \(\widehat{KBF}=\widehat{CBK}\)
ta lại có: \(\widehat{FKB}=\widehat{CBK}\)( so le trong)
=> \(\widehat{KBF}=\widehat{FKB}\)
=> \(\Delta FKB\) cân
=> FK=FB=BE (\(\Delta ABF=\Delta CBE\))
=> BE=FK=AF+AK=EC+AK
VM
5 tháng 6 2019
Bạn ơi, thế ở câu chứng minh tam giác là trường hợp (2 cạnh góc vuông tương ứng bằng nhau) hả bạn? Vì mình chưa thấy ai lại đề trường hợp cạnh góc vuông - cạnh góc vuông cả.
tham khảo
Trên tia đối tia CD lấy điểm M sao cho CM = AK
Ta có: AK + CE = CM + CE = EM (*)
Xét ∆ ABK và ∆ CBM:
AB = CB (gt)
ˆA=ˆC=900
AK = CM (theo cách vẽ)
Do đó: ∆ ABK = ∆ CBM (c.g.c)
⇒ˆB1=ˆB4
(1)
ˆKBC=900–ˆB1
(2)
Trong tam giác CBM vuông tại C.
ˆM=900–ˆB4
(3)
Từ (1), (2) và (3) suy ra: ˆKBC=ˆM
(4)
ˆKBC=ˆB2+ˆB3
mà ˆB1=ˆB2
(gt)
ˆB1=ˆB4
(chứng minh trên)
Suy ra: ˆB2=ˆB4⇒ˆB2+ˆB3=ˆB3+ˆB4
hay ˆKBC=ˆEBM
(5)
Từ (4) và (5) suy ra: ˆEBM=ˆM
⇒ ∆ EBM cân tại E ⇒ EM = BE (**)
Từ (*) và (**) suy ra: AK + CE = BE