Cho số phức thỏa mãn z ≤ 1 . Đặt A = 2 z - 1 2 + i z . Mệnh đề nào sau đây đúng?
A. A ≤ 1
B. A ≥ 1
C. A < 1
D. A > 1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
11 tháng 4 2017
Đáp án A.
Ta có 
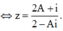
Mà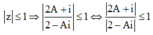 
Đặt A = x + yi, Khi đó (*)
=> |A| ≤ 1.
CM
24 tháng 3 2017
Chọn D.
Giả sử z = x + yi có điểm biểu diễn là M(x; y).
Số phức z - 1có điểm biểu diễn A(x - 1; y) và z - 1 có điểm biểu diễn là B(x; y - 1).
Ta có
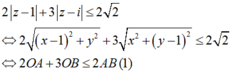
Mà 2OA + 3OB = 2OA + 2OB + OB ≥ 2 AB + OB (2)
Từ (1) và (2) suy ra 2AB + OB ≤ 2AB khi và chỉ khi B và O trùng nhau
Khi đó x; x = 0 và y = 1.
Khi đó z = i ⇒ |z| = 1.
Đáp án A.
Ta có A = 2 z - 1 2 + i z ⇔ 2 A + A i z = 2 z - i ⇔ 2 A + i = 2 z - A i z ⇔ z = 2 A + i 2 - A i .
Mà z ≤ 1 ⇒ 2 A + i 2 - A i ≤ 1 ⇔ 2 A + i 2 - A i ≤ 1 ⇔ 2 A + i ≤ 2 - A i (*).
Đặt A = x + yi, Khi đó (*) ⇔ 2 x + 2 y + 1 i ≤ 2 + y - x i ⇔ 4 x 2 + 2 y + 1 2 ≤ 2 + y 2 + x 2 .
⇔ 4 x 2 + 4 y 2 + 4 y + 1 ≤ x 2 + y 2 + 4 y + 4 ⇔ x 2 + y 2 ≤ 1 ⇒ A ≤ 1 .