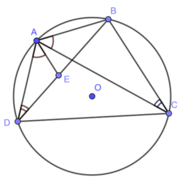
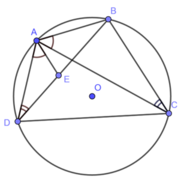
Cho tứ giác ABCD nội tiếp đường tròn (O). Trên đường chéo BD lấy điểm E sao cho ∠ DAE = ∠ BAC . Chứng minh: ∆ ADE ~ ∆ ACE, ∆ ABE ~ ∆ ACD
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
23 tháng 12 2019
Đúng(0)
Những câu hỏi liên quan
18 tháng 3 2021
a) Xét (O) có
ΔADB nội tiếp đường tròn(A,D,B∈(O))
AB là đường kính
Do đó: ΔADB vuông tại D(Định lí)
⇒\(\widehat{ADB}=90^0\)
hay \(\widehat{ADE}=90^0\)
Xét tứ giác ADEH có
\(\widehat{ADE}\) và \(\widehat{AHE}\) là hai góc đối
\(\widehat{ADE}+\widehat{AHE}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ADEH là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
22 tháng 3 2021
a) Xét (O) có
ΔACD nội tiếp đường tròn(A,C,D\(\in\)(O))
AD là đường kính(gt)
Do đó: ΔACD vuông tại C(Định lí)
Suy ra: AC\(\perp\)CD tại C
hay \(EC\perp CD\) tại C
Xét tứ giác ECDF có
\(\widehat{EFD}\) và \(\widehat{ECD}\) là hai góc đối
\(\widehat{EFD}+\widehat{ECD}=180^0\left(90^0+90^0=180^0\right)\)
Do đó: ECDF là tứ giác nội tiếp(Dấu hiệu nhận biết tứ giác nội tiếp)
CH
Cô Hoàng Huyền
Admin
VIP
18 tháng 5 2016
Cô hướng dẫn nhé. :)
Tứ giác AIDE nội tiếp đường tròn đường kính AI.
b. Do câu a ta có AIDE là tứ giác nội tiếp nên gó IDE = góc IAE. Lại có góc IAE = góc CDB. Từ đó suy ra DB là tia phân giac góc CDE.
c. Ta thấy góc CDE = 2 góc CAB (Chứng minh b). Lại có góc COB = 2 góc CAB. Từ đó suy ra góc CDE = góc COB. Hay OEDC là tứ giác nội tiếp ( Góc ngoài ở đỉnh bằng góc đối diện )
Chúc em học tốt ^^