Điểm số trung bình của một vận động viên bắn súng sau 100 lần bắn là 8,69 điểm. Kết quả cụ thể được ghi trong bảng sau, trong đó có hai ô bị mờ không đọc được (đánh dấu *):
Em hãy tìm lại các số trong hai ô đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
15 tháng 1 2017
Gọi số lần bắn đạt điểm 8 là x, số lần bắn đạt điểm 6 là y.
Điều kiện x, y ∈ N; x < 18, y < 18.
Tổng số lần bắn là 100 nên ta có: 25 + 42 + x + 15 + y = 100 ⇔ x + y = 18.
Điểm trung bình là :
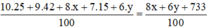
Điểm trung bình bằng 8,69 nên ta có phương trình :
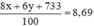⇔ 8x + 6y + 733 = 869 ⇔ 8x + 6y = 136
Ta có hệ phương trình :
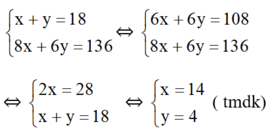
Vậy số lần bắn đạt 8 điểm là 14 và số lần bắn đạt 6 điểm là 4.
4 tháng 4 2017
Gọi số lần bắn được 8 là x
Số lần bắn được 6 là y (x,y\(\in\)N* )
Tổng số lần bắn là 100 . Ta có PT
25+42+x+15+y=100
\(\Leftrightarrow\)x+y=18 (1)
Điểm số trung bình là 8,69 nên ta có PT:
\(\dfrac{10.25+9.42+8x+7.15+6y}{100}=8,69\)
\(\Leftrightarrow\)4x+3y=68(2)
Từ (1) , (2) ta có hệ \(\left\{{}\begin{matrix}x+y=18\\4x+3y-68\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=14\\y=4\end{matrix}\right.\)tmđk
Vậy số lần bắn được điểm 8 là 14 lần
Số lần bắn được điểm 6 là 4 lần
VH
6 tháng 2 2021
a)Số điểm đạt được sau mỗi lần bắn của một xạ thủ.
b) số trung bình cộng: 7,25
c) mốt của dấu hiệu: 8
chúc b học tốt
CM
31 tháng 10 2018
Dấu hiệu : Số điểm đạt được sau mỗi lần bắn của một xạ thủ bắn súng
Đáp án cần chọn là: B
Gọi số lần bắn đạt điểm 8 là x, số lần bắn đạt điểm 6 là y.
Điều kiện x, y ∈ N; x < 18, y < 18.
Tổng số lần bắn là 100 nên ta có: 25 + 42 + x + 15 + y = 100 ⇔ x + y = 18.
Điểm trung bình là :
Điểm trung bình bằng 8,69 nên ta có phương trình :
Ta có hệ phương trình :
Vậy số lần bắn đạt 8 điểm là 14 và số lần bắn đạt 6 điểm là 4.
Kiến thức áp dụng
Giải bài toán bằng cách lập hệ phương trình :
Bước 1 : Lập hệ phương trình
- Chọn các ẩn số và đặt điều kiện thích hợp
- Biểu diễn các đại lượng chưa biết và đã biết theo ẩn
- Lập các phương trình biểu thị mối quan hệ giữa các đại lượng theo đề bài.
- Từ các phương trình vừa lập rút ra được hệ phương trình.
Bước 2 : Giải hệ phương trình (thường sử dụng phương pháp thế hoặc cộng đại số).
Bước 3 : Đối chiếu nghiệm với điều kiện và kết luận.