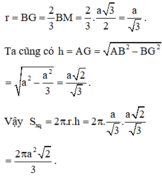Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
r = G H = 1 3 C H = 1 3 . 4 . 3 2 = 2 3 3
h = A G = A C 2 - C G 2 = 4 2 - 4 . 3 2 . 2 3 2 = 4 6 3
S x q = 2 πrl = 2 π . 2 3 3 . 4 6 3 = 16 2 3 π
Đáp án cần chọn là A
Đáp án A
Ta có r t r = G H = 1 3 C H = 2 3 3
h t r u = A G = A C 2 - C G 2 = 4 6 3
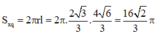
Đáp án A.
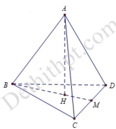
Dựng hình như hình vẽ bên ta có:
Bán kính đường tròn nội tiếp đáy:
r = H M = 1 3 B M = 4 3 6
Chiều cao:
h = A H = A B 2 − B H 2 = 4 2 − 4 3 3 2 = 4 6 3
Do đó S x q T = 2 π h = 16 π 2 3 .
Đáp án D
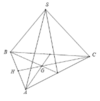
Gọi r là bán kính đường tròn đáy và h là chiều cao tứ diện, ta có Sxq = 2 π .r.h.
Nếu gọi M là trung điểm CD và G là trọng tâm tam giác BCD thì ta có
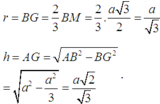
Vậy
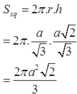
Đáp án D
Gọi r là bán kính đường tròn đáy và h là chiều cao tứ diện, ta có S x q = 2 π . r . h
Nếu gọi M là trung điểm CD và G là trọng tâm tam giác BCD thì ta có
