Cho hình lăng trụ đứng tam giác ABC. A’B’C’, có cạnh bên AA’ = 21 cm, tam giác ABC vuông cân tại A, BC = 42 cm. Tính khoảng cách từ A đến mặt phẳng (A’BC).
A. 21 2 c m
B. 21 2 2 c m
C. 21 2 c m
D. 21 2 4 c m
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

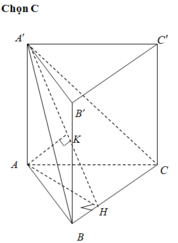
Gọi H là hình chiếu vuông góc của A lên BC.
Gọi K là hình chiếu vuông góc của A lên A’H.
Áp dụng định lí pytago vào tam giác vuông ABC ta tính được AB= a.
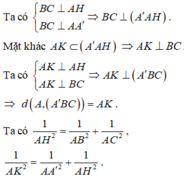
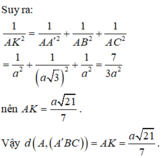

Đáp án A
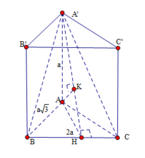
Kẻ đường cao AH của tam giác ABC khi đó B C ⊥ A ' A H , trong Δ A ' A H kẻ đường cao AK thì A K ⊥ A ' B C ta có: A C 2 = 4 a 2 − 3 a 2 = a 2
1 A K 2 = 1 A ' A 2 + 1 A H 2 = 1 A ' A 2 + 1 A B 2 + 1 A C 2 = 1 a 2 + 1 3 a 2 + 1 a 2 = 7 3 a 2

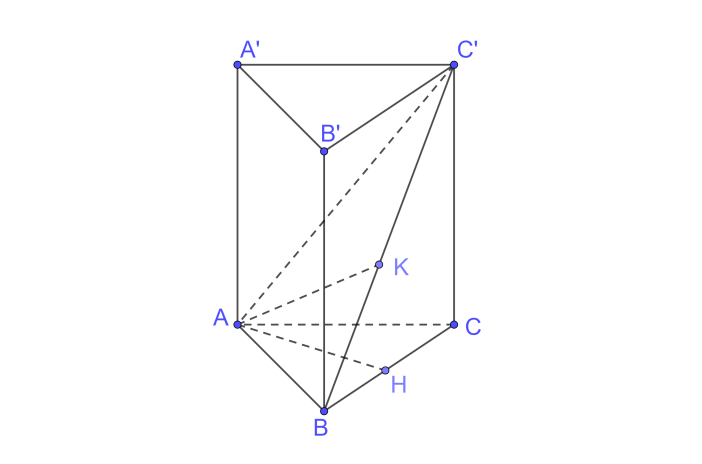
a) Ta có \(BB' \bot \left( {ABC} \right);BB' \subset \left( {BCC'B'} \right) \Rightarrow \left( {ABC} \right) \bot \left( {BCC'B'} \right)\)
\(\left( {ABC} \right) \cap \left( {BCC'B'} \right) = BC\)
(ABC): Kẻ \(AH \bot BC\)
\( \Rightarrow AH \bot \left( {BCC'B'} \right) \Rightarrow d\left( {A,\left( {BCC'B'} \right)} \right) = AH\)
Xét tam giác ABC vuông cân tại A có
\(\frac{1}{{A{H^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{C^2}}} = \frac{2}{{{a^2}}}\) (hệ thức lượng trong tam giác vuông)
\( \Rightarrow AH = \frac{{a\sqrt 2 }}{2}\)
b) +) Ta có \(AB \bot AC,AB \bot AA'\left( {AA' \bot \left( {ABC} \right)} \right) \Rightarrow AB \bot \left( {ACC'A'} \right);AC' \subset \left( {ACC'A'} \right) \Rightarrow AC' \bot AB\)
Do đó tam giác ABC' là tam giác vuông.
+) Trên (ABC’) kẻ \(AK \bot BC' \Rightarrow d\left( {A,BC'} \right) = AK\)
Xét tam giác ACC’ vuông tại C có
\(A{C'^2} = A{C^2} + C{C'^2} = {a^2} + {h^2}\) (Định lí Pytago)
Xét tam giác ABC’ vuông tại A có
\(\begin{array}{l}\frac{1}{{A{K^2}}} = \frac{1}{{A{B^2}}} + \frac{1}{{A{{C'}^2}}} = \frac{1}{{{a^2}}} + \frac{1}{{{a^2} + {h^2}}} = \frac{{2{a^2} + {h^2}}}{{{a^2}\left( {{a^2} + {h^2}} \right)}} \Rightarrow A{K^2} = \frac{{{a^2}\left( {{a^2} + {h^2}} \right)}}{{2{a^2} + {h^2}}}\\ \Rightarrow AK = a.\sqrt {\frac{{{a^2} + {h^2}}}{{2{a^2} + {h^2}}}} \end{array}\)

Đáp án A
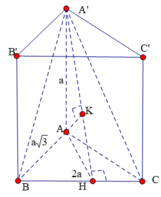
Kẻ đường cao AH của tam giác ABC khi đó BC ⊥ A'AH, trong ∆ A'AH kẻ đường cao AK thì
AK
⊥
(A'BC), ta có: ![]()
![]()
![]()
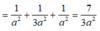

Chọn B.
- Tam giác ABC vuông cân tại A, BC = 42cm
- Tứ diện A.A’BC là tứ diện vuông tại A. Gọi h = d( A, (A’BC)), ta có: