Cho hình lập phương ABCD.A'B'C'D'. Gọi α là góc giữa đường thẳng AC’ với mặt phẳng (ABCd). Mệnh đề nào dưới đây đúng?
A . 2 π 9 ≤ α ≤ π 4
B . π 4 < α < π 3
C . π 6 < α < 2 π 9
D . π 9 ≤ α ≤ π 6
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
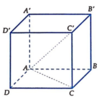
Ta có AC là hình chiếu vuông góc của AC' trên mặt phẳng (ABCD) .
Lại do C C ' ⊥ A B C D nên tam giác C'AC vuông tại C .
Suy ra A C ' , A B C D = A C ' , A C = C ' A C = α .
Ta có tan α = C C ' A C = 2 2 ⇒ π 6 < α < 2 π 9 .
Phân tích phương án nhiễu
Phương án A: Sai do HS tính được tan α 2 2 và cho rằng α = π 4 .
Phương án B: Sai do HS tính sai tan α = A C A C ' = 2 nên suy ra π 4 < α < π 3 .
Phương án D: Sai do HS tính sai tan α = C C ' A C ' = 3 3 nên suy ra α = π 6 .

Đáp án D
Gọi I là giao điểm của AC và BD
A I ⊥ B D A I ⊥ B B ' ⇒ A I ⊥ ( B B ' D ' D ) ⇒ B’I là hình chiếu vuông góc của AB’ lên (BB’D’D)
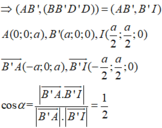

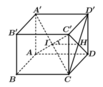
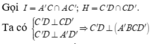
=> IH là hình chiếu vuông góc của IC' trên mặt phẳng A ' B C D '
Do đó ![]()
Trong tam giác vuông C'HI, có 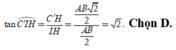
Đáp án C.
Ta có AC là hình chiếu vuông góc của A'C trên mặt phẳng (ABCD).
Lại do CC' ⊥ (ABCD) nên tam giác C'AC vuông tại C
Suy ra
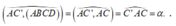
Ta có
Phân tích phương án nhiễu
Phương án A: Sai do HS tính được tan α 2 2 và cho rằng α = π 4
Phương án B: Sai do HS tính sai tan α = A C A C ' = 2 nên suy ra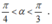
Phương án D: Sai do HS tính sai tan α = C C ' A C ' = 3 3 nên suy ra α = π 6