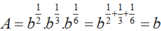Đơn giản biểu thức ![]() ( b>0) ta được:
( b>0) ta được:
A. A= b2
B. A = b 3
C. A = b
D. A = b 2 3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(M=a^2-a\left|a\right|-\dfrac{b}{2}\cdot2\left|b\right|-b^2\\ M=a^2+a^2-b^2-b^2\\ M=2\left(a^2-b^2\right)\\ D\)

Bài 4: Đơn giản các biểu thức sau khi bỏ dấu ngoặc
a/ (a + b - c) - (b - c + d)
= a + b - c - b +c - d
= a + (b - b) + (-c + c) - d
= a - d
b/ -(a-b+c)+(a-b+d)
= -a + b - c + a - b + d
= (-a + a) + (b - b) - c + d
= -c + d
c/ (a+b)-(-a+b-c)
= a + b + a - b + c
= 2a + c
d/ -(a+b) + (a+b+c)
= -a - b + a + b + c
= c

( a + b + c)3 + (a - b - c)3 - 6a( b+ c)2
= ( a+ b + c + a - b - c)[ (a+b+c)2 + (a+b+c)(a-b-c) + (a-b-c)2 ] - 6a( b+c)2
= 2a [ a2 + b2 + c2 + 2ab+ 2bc+ 2ac + a2 - ( b+ c)2 + a2 + b2 + c2 - 2ab - 2ac + 2bc] - 6a ( b+c)2
= 2a [ 3a2 + 2b2 + 2c2 + 4bc - (b+c)2 - 3(b+c)2}
= 2a ( 3a2 + 2b2 + 2c2 - 4( b+ c)2 + 4bc}

bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....

a) (a + b - c) - (b - c + d)
= a + b - c - b + c - d
= a + (b - b) - (c - c) - d
= a + 0 - 0 - d
= a - d
b) -(a + b + c) + (a - b + d)
= -a - b - c + a - b + d
= (-a + a) + (-b - b) - c + d
= -2b - c + d
câu c) tương tự nhé!! 34656654745756876876457567568687687698798363645765756
a) (a + b - c) - (b - c + d)
= a + b - c - b + c - d
= a - d
b) -(a - b + c) + (a - b + d)
= -a + b - c + a - b + d
= -c + d
= d - c
c) (a + b) - (-a + b - c)
= a + b + a - b + c
= 2a + c
Chọn C.
Ta có: