Cho tứ diện ABCD, xét điểm M they đổi trên cạnh AB (M≠A, M≠B). Gọi (P) là mặt phẳng đi qua M, song song với AC và BD. Thiết diện của tứ diện với mặt phẳng (P) có diện tích lớn nhất thì tỉ số AM/AB bằng
A. 1 2
B. 1 3
C. 1 4
D. 3 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

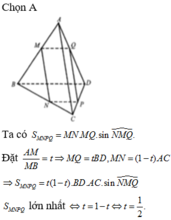

Đáp án B
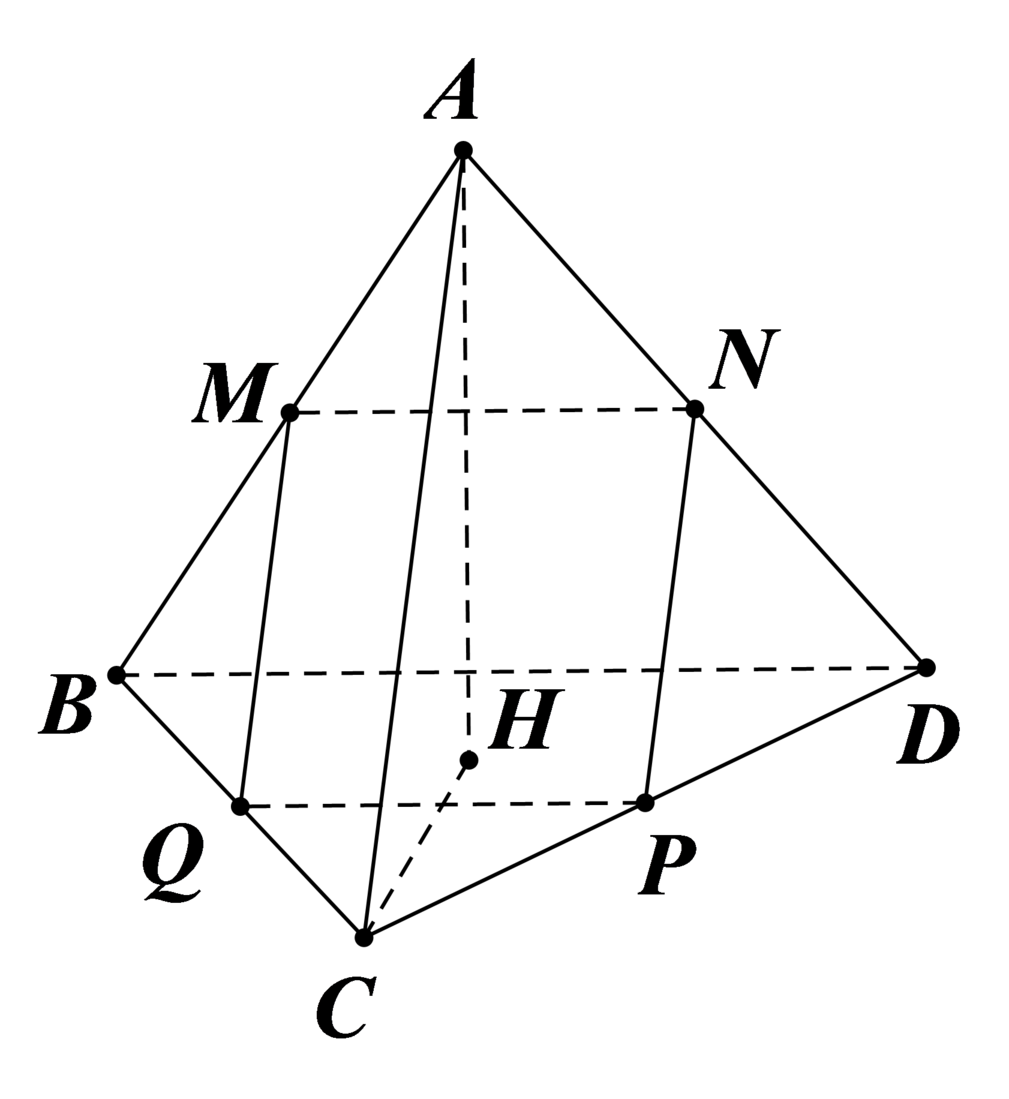
Gọi N, P, Q lần lượt là trung điểm của Ad, CD, BC.
Ta có: B D ⊥ A H C nên B D ⊥ A C . Do đó M N ⊥ N P . Mà MNPQ là hình bình hành.
Thiết diện là hình vuông MNPQ.

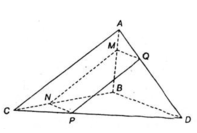
a) + (α) // AC
⇒ Giao tuyến của (α) và (ABC) là đường thẳng song song với AC.
Mà M ∈ (ABC) ∩ (α).
⇒ (ABC) ∩ (α) = MN là đường thẳng qua M, song song với AC (N ∈ BC).
+ Tương tự (α) ∩ (ABD) = MQ là đường thẳng qua M song song với BD (Q ∈ AD).
+ (α) ∩ (BCD) = NP là đường thẳng qua N song song với BD (P ∈ CD).
+ (α) ∩ (ACD) = QP.
b)Ta có:
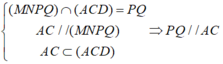
Suy ra, tứ giác MNPQ có các cạnh đối song song với nhau nên tứ giác MNPQ là hình bình hành.