Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
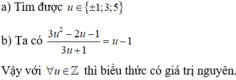
Vì 3 / (x + 2) là một số nguyên nên 3 ⋮ (x + 2) và x ≠ - 2
Suy ra: x + 2 ∈ Ư(3) = {- 3; - 1; 1; 3}
Ta có: x + 2 = - 3 ⇒ x = - 5; x + 2= - 1 ⇒ x = - 3
x + 2 = 1 ⇒ x = -1; x + 2 = 3 ⇒ x = 1
Vậy với x ∈ {-5; -3; -1; 1} thì 3 / (x + 2) là một số nguyên.
Ta có:
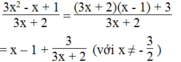
Vì x là số nguyên nên x – 1 là số nguyên.
Để biểu thức đã cho là số nguyên thì 3 ⋮ (3x + 2) và x ≠ -2/3
Suy ra: 3x + 2 ∈ Ư(3) = {-3; -1; 1; 3}
Ta có: 3x + 2 = -3 ⇒ x = -5/3 ∉ Z (loại)
3x + 2 = -1 ⇒ x = - 1
3x + 2 = 1 ⇒ x = -1/3 ∉ Z (loại)
3x + 2 = 3 ⇒ x = 1/3 ∉ Z (loại)
x = -1 khác -3/2
Vậy với x = - 1 thì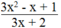
có giá trị nguyên.
Vì 2 / (x - 3) là một số nguyên nên 2 ⋮ (x – 3) và x ≠ 3
Suy ra: x – 3 ∈ Ư(2) = {- 2; - 1; 1; 2}
Ta có:x – 3 = - 2 ⇒ x = 1; x – 3 = - 1 ⇒ x = 2
x – 3 = 1 ⇒ x = 4; x – 3 = 2 ⇒ x = 5
Vậy với x ∈ {1; 2; 4; 5} thì 2 / (x - 3) là một số nguyên.
Ta có:
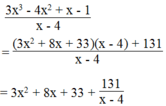
Với x là số nguyên ta có: 3 x 2 + 8 x + 33 là số nguyên.
Để biểu thức đã cho là số nguyên thì 131 ⋮ (x – 4) và x ≠ 4
Suy ra: x – 4 ∈ Ư(131) = {-131; -1; 1; 131}
Ta có: x – 4 = -131 ⇒ x = -127; x – 4 = -1 ⇒ x = 3
x – 4 = 1 ⇒ x = 5; x – 4 = 131 ⇒ x = 135
Vậy với x ∈ {-127; 3; 5; 135} thì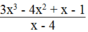 
là số nguyên.
\(A=\frac{x^3-x^2+2}{x-1}=x^2+\frac{2}{x-1}\inℤ\Leftrightarrow\frac{2}{x-1}\inℤ\)
mà \(x\inℤ\)nên \(x-1\inƯ\left(2\right)=\left\{-2,-1,1,2\right\}\)
\(\Leftrightarrow x\in\left\{-1,0,2,3\right\}\).
c) ĐKXĐ : \(x\ne4\)
Để biểu thức \(\frac{3x^3-4x^2+x-1}{x-4}\) nguyên với \(x\) nguyên thì :
\(3x^3-4x^2+x-1⋮x-4\)
\(\Leftrightarrow3x^3-12x^2+8x^2-32x+33x-132+131⋮x-4\)
\(\Leftrightarrow3x^2.\left(x-4\right)+8x.\left(x-4\right)+31.\left(x-4\right)+131⋮x-4\)
\(\Leftrightarrow131⋮x-4\)
\(\Leftrightarrow x-4\inƯ\left(131\right)\)
\(\Leftrightarrow x-4\in\left\{-1,1,131,-131\right\}\)
\(\Leftrightarrow x\in\left\{3,5,135,-127\right\}\)
d) ĐKXĐ : \(x\ne-\frac{3}{2}\)
Để biểu thức \(\frac{3x^2-x+1}{3x+2}\) nhận giá trị nguyên với \(x\) nguyên thì :
\(3x^2-x+1⋮3x+2\)
\(\Leftrightarrow3x^2+2x-3x-2+3⋮3x+2\)
\(\Leftrightarrow x.\left(3x+2\right)-\left(3x+2\right)+3⋮3x+2\)
\(\Leftrightarrow3⋮3x+2\)
\(\Leftrightarrow3x+2\inƯ\left(3\right)\)
\(\Leftrightarrow3x+2\in\left\{-1,1,-3,3\right\}\)
\(\Leftrightarrow x\in\left\{-1,-\frac{1}{3},-\frac{5}{3},\frac{1}{3}\right\}\) mà \(x\) nguyên
\(\Rightarrow x=-1\)
