Trong mặt phẳng tọa độ Oxy, cho ba điểm A(-4; 0); B(-5; 0) và C(3; 0). Tìm điểm M thuộc trục hoành sao cho M A → + M B → + M C → = 0 → .
A. M (-2; 0)
B. M(2; 0)
C. M(- 4; 0)
D. M(- 5; 0)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\left\{{}\begin{matrix}x_G=\dfrac{-1+\left(-2\right)+4}{3}=\dfrac{1}{3}\\y_G=\dfrac{1+3+\left(-5\right)}{3}=-\dfrac{1}{3}\end{matrix}\right.\)

Ta có A B → = − 1 ; 11 , A C → = − 7 ; 3 .
Suy ra A B → . A C → = − 1 . − 7 + 11.3 = 40.
Chọn A.

Ta có A B → = − 1 ; 11 , A C → = − 7 ; 3 .
Suy ra A B → . A C → = − 1 . − 7 + 11.3 = 40.
Chọn A.

a) Ta có:
\(\left\{ \begin{array}{l}\overrightarrow {AB} = (2 - ( - 4);4 - 1) = (6;3)\\\overrightarrow {BC} = (2 - 2; - 2 - 4) = (0; - 6)\\\overrightarrow {AC} = (2 - ( - 4); - 2 - 1) = (6; - 3)\end{array} \right.\)\( \Rightarrow \left\{ \begin{array}{l}AB = \left| {\overrightarrow {AB} } \right| = \sqrt {{6^2} + {3^2}} = 3\sqrt 5 \\BC = \left| {\overrightarrow {BC} } \right| = \sqrt {{0^2} + {{( - 6)}^2}} = 6\\AC = \left| {\overrightarrow {CA} } \right| = \sqrt {{6^2} + {{( - 3)}^2}} = 3\sqrt 5 .\end{array} \right.\)
Áp dụng định lí cosin cho tam giác ABC, ta có:
\(\cos \widehat A = \frac{{{b^2} + {c^2} - {a^2}}}{{2bc}} = \frac{{{{\left( {3\sqrt 5 } \right)}^2} + {{\left( {3\sqrt 5 } \right)}^2} - {{\left( 6 \right)}^2}}}{{2.3\sqrt 5 .3\sqrt 5 }} = \frac{3}{5}\)\( \Rightarrow \widehat A \approx 53,{13^o}\)
\(\cos \widehat B = \frac{{{a^2} + {c^2} - {b^2}}}{{2ac}} = \frac{{{{\left( 6 \right)}^2} + {{\left( {3\sqrt 5 } \right)}^2} - {{\left( {3\sqrt 5 } \right)}^2}}}{{2.6.3\sqrt 5 }} = \frac{{\sqrt 5 }}{5}\)\( \Rightarrow \widehat B \approx 63,{435^o}\)
\( \Rightarrow \widehat C \approx 63,{435^o}\)
Vậy tam giác ABC có: \(a = 6;b = 3\sqrt 5 ;c = 3\sqrt 5 \); \(\widehat A \approx 53,{13^o};\widehat B = \widehat C \approx 63,{435^o}.\)
b)
Gọi H có tọa độ (x; y)
\( \Rightarrow \left\{ \begin{array}{l}\overrightarrow {AH} = (x - ( - 4);y - 1) = (x + 4;y - 1)\\\overrightarrow {BH} = (x - 2;y - 4)\end{array} \right.\)
Lại có: H là trực tâm tam giác ABC
\( \Rightarrow AH \bot BC\) và \(BH \bot AC\)
\( \Rightarrow \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {AH} ,\overrightarrow {BC} } \right) = 0\) và \(\left( {\overrightarrow {BH} ,\overrightarrow {AC} } \right) = {90^o} \Leftrightarrow \cos \left( {\overrightarrow {BH} ,\overrightarrow {AC} } \right) = 0\)
Do đó \(\overrightarrow {AH} .\overrightarrow {BC} = \overrightarrow 0 \) và \(\overrightarrow {BH} .\overrightarrow {AC} = \overrightarrow 0 \).
Mà: \(\overrightarrow {BC} = (0; - 6)\)
\( \Rightarrow (x + 4).0 + (y - 1).( - 6) = 0 \Leftrightarrow - 6.(y - 1) = 0 \Leftrightarrow y = 1.\)
Và \(\overrightarrow {AC} = (6; - 3)\)
\(\begin{array}{l} \Rightarrow (x - 2).6 + (y - 4).( - 3) = 0\\ \Leftrightarrow 6x - 12 + ( - 3).( - 3) = 0\\ \Leftrightarrow 6x - 3 = 0\\ \Leftrightarrow x = \frac{1}{2}.\end{array}\)
Vậy H có tọa độ \(\left( {\frac{1}{2}}; 1 \right)\)

a: A(2;4); B(1;0); C(2;2)
vecto AB=(-1;-4)
vecto DC=(2-x;2-y)
Vì ABCD là hình bình hành nên vecto AB=vecto DC
=>2-x=-1 và 2-y=-4
=>x=3 và y=6
c: N đối xứng B qua C
=>x+1=4 và y+0=4
=>x=3 và y=4

a: 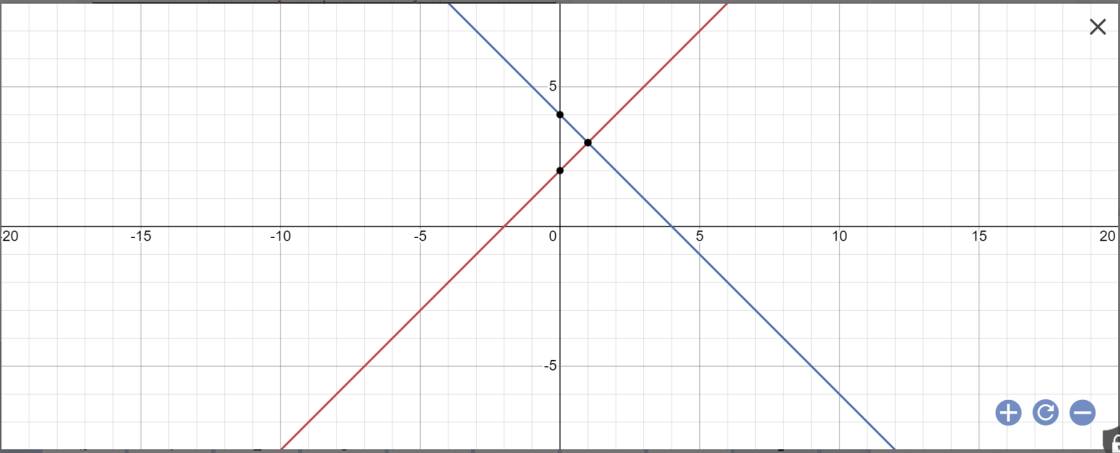
b: Tọa độ giao điểm của (d1) và (d2) là:
\(\left\{{}\begin{matrix}x+2=-x+4\\y=x+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x=2\\y=x+2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=1+2=3\end{matrix}\right.\)
Thay x=1 và y=3 vào (d3), ta được:
\(1\cdot m+m=3\)
=>2m=3
=>\(m=\dfrac{3}{2}\)

Đáp án C
Gọi I(x;y;0) là tâm của mặt cầu (S) ⇒ A I → = x - 1 ; y - 2 ; 4 A I → = x - 1 ; y + 3 ; - 1 A I → = x - 2 ; y - 2 ; - 3
Theo bài ra, ta có
I A = I B I A = I C ⇒ x - 1 2 + y - 2 2 + 4 2 = x - 1 2 + y + 3 2 + - 1 2 x - 1 2 + y - 2 2 + 4 2 = x - 2 2 + y - 2 2 + - 3 2 ⇔ x = - 2 y = 1
Vậy I ( - 2 ; 1 ; 0 ) ⇒ A I → = ( - 3 ; - 1 ; 4 ) ⇒ l = 2 . I A = 2 16 .

Chọn C
Gọi tâm mặt cầu là: I(x;y;0).
I A = I B I A = I C ⇔ ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 1 ) 2 + ( y + 3 ) + 1 2 ( x - 1 ) 2 + ( y - 2 ) 2 + 4 2 = ( x - 2 ) 2 + ( y - 2 ) 2 + 3 2 ⇔ ( y - 2 ) 2 + 4 2 = ( y + 3 ) 2 + 1 2 x 2 - 2 x + 1 + 16 = x 2 - 4 x + 4 + 9 ⇔ 10 y = 10 2 x = - 4 ⇔ x = - 2 y = 1 ⇒ i = 2 R = 2 ( - 3 ) 2 + ( - 1 ) 2 + 4 2 = 2 26
Ta có M ∈ O x nên M(x;O) và M A → = − 4 − x ; 0 M B → = − 5 − x ; 0 M C → = 3 − x ; 0 ⇒ M A → + M B → + M C → = − 6 − 3 x ; 0 .
Do M A → + M B → + M C → = 0 → nên − 6 − 3 x = 0 ⇔ x = − 2 ⇒ M − 2 ; 0 .
Chọn A.