Xét dấu của biểu thức sau : f(x) = x4 – 4x + 1 A. 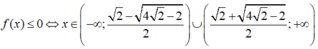B. 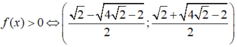C. ...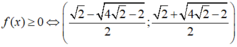
Đọc tiếp
Xét d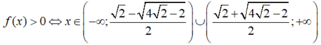ấu của biểu thức sau : f(x) = x4 – 4x + 1
A. 
B. 
C. 
D. 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
CM
21 tháng 6 2017
f(x) = (3x2 – 4x)(2x2 – x – 1)
+ Tam thức 3x2 – 4x có hai nghiệm x = 0 và x = 4/3, hệ số a = 3 > 0.
Do đó 3x2 – 4x mang dấu + khi x < 0 hoặc x > 4/3 và mang dấu – khi 0 < x < 4/3.
+ Tam thức 2x2 – x – 1 có hai nghiệm x = –1/2 và x = 1, hệ số a = 2 > 0
Do đó 2x2 – x – 1 mang dấu + khi x < –1/2 hoặc x > 1 và mang dấu – khi –1/2 < x < 1.
Ta có bảng xét dấu:
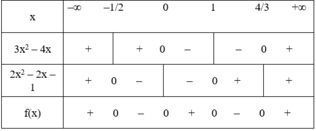
Kết luận:
f(x) > 0 ⇔ x ∈ (–∞; –1/2) ∪ (0; 1) ∪ (4/3; +∞)
f(x) = 0 ⇔ x ∈ {–1/2; 0; 1; 4/3}
f(x) < 0 ⇔ x ∈ (–1/2; 0) ∪ (1; 4/3)
PT
1
HQ
Hà Quang Minh
Giáo viên
26 tháng 9 2023
a) \(f\left( x \right) = 2{x^2} + 4x + 2\) có \(\Delta = 0\), có nghiệm kép là \({x_1} = {x_2} = - 1\)
và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
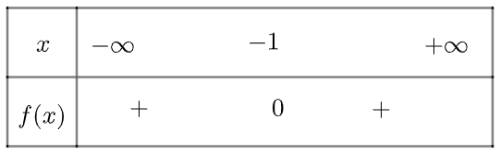
Vậy \(f\left( x \right)\) dương với mọi \(x \ne - 1\)
b) \(f\left( x \right) = - 3{x^2} + 2x + 21\) có \(\Delta = 256 > 0\), hai nghiệm phân biệt là \({x_1} = - \frac{7}{3};{x_2} = 3\)
và \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
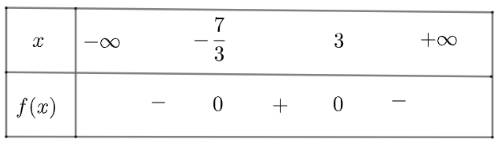
Vậy \(f\left( x \right)\) dương với \(x \in \left( { - \frac{7}{3};3} \right)\) và âm khi \(x \in \left( { - \infty ; - \frac{7}{3}} \right) \cup \left( {3; + \infty } \right)\)
c) \(f\left( x \right) = - 2{x^2} + x - 2\) có \(\Delta = - 15 < 0\), tam thức vô nghiệm
và \(a = - 2 < 0\)
Ta có bảng xét dấu như sau:
Vậy \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
d) \(f\left( x \right) = - 4x\left( {x + 3} \right) - 9 = - 4{x^2} - 12x - 9\) có \(\Delta = 0\), tam thức có nghiệm kép \({x_1} = {x_2} = - \frac{3}{2}\) và \(a = - 4 < 0\)
Ta có bảng xét dấu như sau
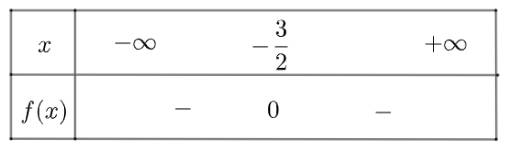
Vậy \(f\left( x \right)\) âm với mọi \(x \ne - \frac{3}{2}\)
e) \(f\left( x \right) = \left( {2x + 5} \right)\left( {x - 3} \right) = 2{x^2} - x - 15\) có \(\Delta = 121 > 0\), có hai nghiệm phân biệt \({x_1} = - \frac{5}{2};{x_2} = 3\) và có \(a = 2 > 0\)
Ta có bảng xét dấu như sau
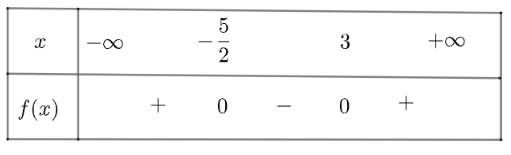
Vậy \(f\left( x \right)\) âm với \(x \in \left( { - \frac{5}{2};3} \right)\) và dương khi \(x \in \left( { - \infty ; - \frac{5}{2}} \right) \cup \left( {3; + \infty } \right)\)
PT
1
CM
15 tháng 2 2018
f(x) = (3x2 – 10x + 3)(4x – 5)
+ Tam thức 3x2 – 10x + 3 có hai nghiệm x = 1/3 và x = 3, hệ số a = 3 > 0 nên mang dấu + nếu x < 1/3 hoặc x > 3 và mang dấu – nếu 1/3 < x < 3.
+ Nhị thức 4x – 5 có nghiệm x = 5/4.
Ta có bảng xét dấu:
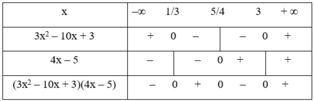
Kết luận:
f(x) > 0 khi x ∈ (1/3; 5/4) ∪ x ∈ (3; +∞)
f(x) = 0 khi x ∈ {1/3; 5/4; 3}
f(x) < 0 khi x ∈ (–∞; 1/3) ∪ (5/4; 3)
14 tháng 12 2023
a: Đặt f(x)=0
=>\(-3x^2+2x=0\)
=>\(3x^2-2x=0\)
=>x(3x-2)=0
=>\(\left[{}\begin{matrix}x=0\\3x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{2}{3}\end{matrix}\right.\)
Bảng xét dấu:
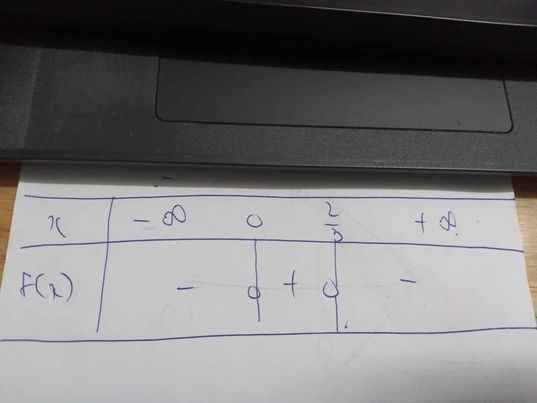
b: Đặt G(x)=0
=>\(x^2-10x+25=0\)
=>\(\left(x-5\right)^2=0\)
=>x-5=0
=>x=5
Bảng xét dấu:
c: Đặt H(x)=0
=>\(4x^2-4x+1=0\)
=>\(\left(2x-1\right)^2=0\)
=>2x-1=0
=>x=1/2
Bảng xét dấu:
d: Đặt Q(x)=0
=>(2x+3)(x-5)=0
=>\(\left[{}\begin{matrix}2x+3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=5\end{matrix}\right.\)
Bảng xét dấu:
CM
15 tháng 4 2018
Đáp án: B
Ta có bảng xét dấu:
Dựa vào bảng xét dấu ta thấy: f(x) > 0 khi x < -7 hoặc -1 < x < 1 hoặc x > 3
N
20 tháng 11 2021
Đặt \(g\left(x\right)=f\left(x\right)-10\) (bậc 4)
\(\Leftrightarrow\left\{{}\begin{matrix}g\left(1\right)=0\\g\left(2\right)=0\\g\left(3\right)=0\end{matrix}\right.\Leftrightarrow g\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)\) (m là hằng số)
\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-m\right)-10\\ \Leftrightarrow f\left(9\right)=8\cdot7\cdot6\left(9-m\right)-10=336\left(9-m\right)-10\\ f\left(-5\right)=\left(-6\right)\left(-7\right)\left(-8\right)\left(-5-m\right)-10=336\left(m+5\right)-10\)
Vậy \(A=336\left(9-m\right)+336\left(m+5\right)-20=4684\)
Chúc bạn hok tốt <3
25 tháng 6 2023
1: A=(x-1)^2>=0
Dấu = xảy ra khi x=1
5: B=-(x^2+6x+10)
=-(x^2+6x+9+1)
=-(x+3)^2-1<=-1
Dấu = xảy ra khi x=-3
2: B=x^2+4x+4-9
=(x+2)^2-9>=-9
Dấu = xảy ra khi x=-2
6: =-(x^2-5x-3)
=-(x^2-5x+25/4-37/4)
=-(x-5/2)^2+37/4<=37/4
Dấu = xảy ra khi x=5/2
3: =x^2+x+1/4-1/4
=(x+1/2)^2-1/4>=-1/4
Dấu = xảy ra khi x=-1/2
7: =4x^2+4x+1-2
=(2x+1)^2-2>=-2
Dấu = xảy ra khi x=-1/2
Chọn D