Cho tam giác ABC cân tại A. Về phía ngoài tam giác ABC vẽ hai tam giác đều ACD và ABE. So sánh BD và CE.
A. BD = CE
B. BD > CE
C. BD < CE
D. BD = 2CE
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
27 tháng 11 2017
Đúng(0)
Những câu hỏi liên quan
23 tháng 1 2022
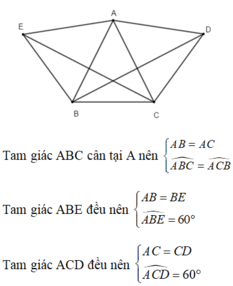
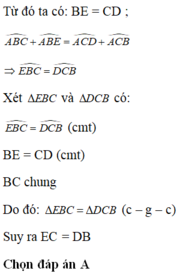
a: Xét ΔBAD và ΔEAC có
BA=EA
\(\widehat{BAD}=\widehat{EAC}\)
AD=AC
Do đó: ΔBAD=ΔEAC
Suy ra: BD=EC
b: \(\widehat{BOC}=90^0\)
4 tháng 7 2017
a/ ta có \(\hept{\begin{cases}\widehat{ACE}=\widehat{BCE}=\widehat{\frac{ACB}{2}}\\\widehat{ABD}=\widehat{CBD}=\widehat{\frac{ABC}{2}}\end{cases}}\)( tia phân giác )
mà \(\widehat{ACB}=\widehat{ABC}\)( tam giác cân)
nên ACE=BCE=ABD=CBD
xét tam giác ABD và tam giác ACE có
ABD=ACE(cmt) ; góc A chung ; AB=AC(tam giác cân)
=> tam giác ABD=tam giác ACE (G-C-G) => BD=CE
b/ ta có BCE=CBD (cmt) => tam giác BIC cân tại I
xét tam giácBIE và tam giác CID có
BI=IC(tam giác BIC cân) ; BIE=ICD(ABD=ACE) ; BIE=CID(2 góc đối đỉnh)
=> tam giác BIE= tam giác CID (G-C-G)
c/ ta có BD, CE là tia p/g cắt nhau tại I => I là gđ của 3 đg phân giác của tam giác ABC
=> AI là tia phân giác của BAC
ta có AB=AE+BE ; AC=AD+DC
mà BE=CD ( tam giác BIE= tam giác CID) ; AB=AC (tam giác ABC cân)
nên AE=AD => tam giác AED cân
mặt khác AI là tia phân giác => AI là đường cao => AI vuông góc vs ED
ta có \(\hept{\begin{cases}\widehat{AED}=\frac{180^0-\widehat{A}}{2}\\\widehat{ABC}=\frac{180^0-\widehat{A}}{2}\end{cases}}\)(tam giác cân)
=> AED=ABC
mà 2 góc nằm ở vị trí đồng vị => ED//BC
4 tháng 7 2017
A) Ta có \(\Delta\)ABC cân tại A =>góc ABC= góc ACB => \(\frac{1}{2}\)góc ABC =\(\frac{1}{2}\)góc ACB => góc DBC = góc ECB = góc DBE = góc DCE
Xét \(\Delta\)ECB và \(\Delta\)DBC có
-góc DBC = góc ECB
- BC chung
-góc EBC = góc DCB
=> \(\Delta\)ECB = \(\Delta\)DBC ( g.c.g )
=> CE =BD
B, Ta có góc IBC = góc ICB ( góc DBC =góc ECB chứng minh trên )
=> \(\Delta\)IBC cân tại I => BI = CI
Xét \(\Delta\)BIE và \(\Delta\)CID có
- góc BIE = góc CID ( 2 góc đối đỉnh )
- IB =CI ( chứng minh trên )
- góc IBE =ICD ( chứng minh trên ý a )
=> \(\Delta\)BIE =\(\Delta\)CID (g.c.g)
C, Ta có AB =AC ( \(\Delta\)ABC cân tại A )
Mà BE =CD ( \(\Delta\) EBD =\(\Delta\)DCE )
=> AE =AD (1)
Lại có BD =CE ( chứng minh trên ý a )
Mà BI =CI ( chứng minh trên )
=> EI =ID (2)
Từ (1) và (2) => AI là đường trung trực của ED
=> AI \(⊥\)ED
Ta có \(\Delta\)EAD cân tại A có Ai là đường phân giác => góc EAI = góc DAI
Lại có \(\Delta\)ABC cân tại A có AI là tia phân giác đồng thời là đường cao => AI \(⊥\)BC
\(\hept{\begin{cases}AI⊥DE\\AI⊥BC\end{cases}}\)
=> ED sog sog BC
Chúc bạn học giỏi
Kết bạn với mình nha