Giá trị nhỏ nhất của biểu thức x2+y2 -2x+4y+8 là : A.8. B.3. C.-3. D. -8. Giải thích cách làm hộ mình cái 😰😰
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
82
2
TN
24 tháng 6 2016
nè bạn Câu hỏi của Hương Linh - Toán lớp 8 - Học toán với OnlineMath
13 tháng 6 2023
1:
=x^2-6x+9-4=(x-3)^2-4>=-4
Dấu = xảy ra khi x=3
3: =-y^2-4y-4+13
=-(y+2)^2+13<=13
Dấu = xảy ra khi y=-2
4: D=x^2-8>=-8
Dấu = xảy ra khi x=0
22 tháng 11 2023
Bài 1:
a: \(A=x^2+2x+4\)
\(=x^2+2x+1+3\)
\(=\left(x+1\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x+1=0
=>x=-1
Vậy: \(A_{min}=3\) khi x=-1
b: \(B=x^2-20x+101\)
\(=x^2-20x+100+1\)
\(=\left(x-10\right)^2+1>=1\forall x\)
Dấu '=' xảy ra khi x-10=0
=>x=10
Vậy: \(B_{min}=1\) khi x=10
c: \(C=x^2-2x+y^2+4y+8\)
\(=x^2-2x+1+y^2+4y+4+3\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+3>=3\forall x\)
Dấu '=' xảy ra khi x-1=0 và y+2=0
=>x=1 và y=-2
Vậy: \(C_{min}=3\) khi (x,y)=(1;-2)
Bài 2:
a: \(A=5-8x-x^2\)
\(=-\left(x^2+8x\right)+5\)
\(=-\left(x^2+8x+16-16\right)+5\)
\(=-\left(x+4\right)^2+16+5=-\left(x+4\right)^2+21< =21\forall x\)
Dấu '=' xảy ra khi x+4=0
=>x=-4
b: \(B=x-x^2\)
\(=-\left(x^2-x\right)\)
\(=-\left(x^2-x+\dfrac{1}{4}-\dfrac{1}{4}\right)\)
\(=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}< =\dfrac{1}{4}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{2}=0\)
=>\(x=\dfrac{1}{2}\)
c: \(C=4x-x^2+3\)
\(=-x^2+4x-4+7\)
\(=-\left(x^2-4x+4\right)+7\)
\(=-\left(x-2\right)^2+7< =7\forall x\)
Dấu '=' xảy ra khi x-2=0
=>x=2
d: \(D=-x^2+6x-11\)
\(=-\left(x^2-6x+11\right)\)
\(=-\left(x^2-6x+9+2\right)\)
\(=-\left(x-3\right)^2-2< =-2\forall x\)
Dấu '=' xảy ra khi x-3=0
=>x=3
TL
1
23 tháng 10 2021
\(a,=3\left(x^2-x+\dfrac{1}{4}\right)+\dfrac{1}{4}=3\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\ge\dfrac{1}{4}\)
Dấu \("="\Leftrightarrow x=\dfrac{1}{2}\)
\(b,=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+1=\left(x-1\right)^2+\left(y+2\right)^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
\(c,=\left(x^2-2xy+y^2\right)+x^2+1=\left(x-y\right)^2+x^2+1\ge1\)
Dấu \("="\Leftrightarrow\left\{{}\begin{matrix}x=y\\x=0\end{matrix}\right.\Leftrightarrow x=y=0\)
23 tháng 10 2016
bài 5 nhé:
a) (a+1)2>=4a
<=>a2+2a+1>=4a
<=>a2-2a+1.>=0
<=>(a-1)2>=0 (luôn đúng)
vậy......
b) áp dụng bất dẳng thức cô si cho 2 số dương 1 và a ta có:
a+1>=\(2\sqrt{a}\)
tương tự ta có:
b+1>=\(2\sqrt{b}\)
c+1>=\(2\sqrt{c}\)
nhân vế với vế ta có:
(a+1)(b+1)(c+1)>=\(2\sqrt{a}.2\sqrt{b}.2\sqrt{c}\)
<=>(a+1)(b+1)(c+1)>=\(8\sqrt{abc}\)
<=>(a+)(b+1)(c+1)>=8 (vì abc=1)
vậy....
AH
Akai Haruma
Giáo viên
11 tháng 1 2021
Lời giải:
a)
$A=4x^2+4x+11=(4x^2+4x+1)+10=(2x+1)^2+10\geq 10$
Vậy $A_{\min}=10$. Giá trị này đạt tại $(2x+1)^2=0$
$\Leftrightarrow x=-\frac{1}{2}$
b)
$C=x^2-2x+y^2-4y+7=(x^2-2x+1)+(y^2-4y+4)+2$
$=(x-1)^2+(y-2)^2+2\geq 2$
Vậy $C_{\min}=2$. Giá trị này đạt tại $(x-1)^2=(y-2)^2=0$
$\Leftrightarrow x=1; y=2$
CM
26 tháng 2 2019
Đáp án D
Phương pháp:
+ Tìm tâm và bán kính của mặt cầu
+ Xác định vị trí tương đối của mặt phẳng và mặt cầu để suy ra vị trí của điểm M
+ Tìm tọa độ của đường thẳng và mặt cầu thì ta giải hệ phương trình gồm phương trình đường thẳng và phương trình mặt cầu
Cách giải:
Mặt cầu (S) có tâm
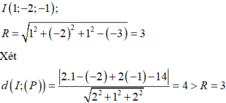
nên mặt phẳng (P) không cắt mặt cầu (S).Khi đó điểm M thuộc mặt cầu (S) sao cho khoảng cách từ M đến mặt phẳng (P) là nhỏ nhất thì M là giao điểm của đường thẳng d đi qua I , nhận n P → = 2 ; - 1 ; 2 làm VTCP với mặt cầu.
Phương trình đường thẳng
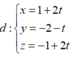
Tọa độ giao điểm của đường thẳng d và mặt cầu (S) thỏa mãn hệ phương trình
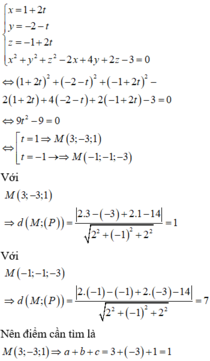
\(x^2+y^2-2x+4y+8=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+3\)
\(=\left(x-1\right)^2+\left(y+2\right)^2+3\ge3\)
Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)
Vậy GTNN là 3 khi x=1 và y=-2
=>Chọn B
\(x^2+y^2-2x+4y+8=\left(x^2-2x+1\right)+\left(y^2+4y+4\right)+3=\left(x-1\right)^2+\left(y+2\right)^2+3\ge3\)
Dấu "=" \(\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=-2\end{matrix}\right.\)