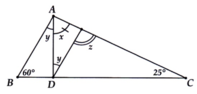
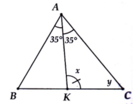
Tính số đo x, y, z trong các hình vẽ sau:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
12 tháng 11 2019
Đúng(0)
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
18 tháng 9 2023
Áp dụng định lí tổng ba góc trong tam giác, ta có:
+)
\(\begin{array}{l}x + {120^o} + {35^o} = {180^o}\\ \Rightarrow x + {155^o} = {180^o}\\ \Rightarrow x = {180^o} - {155^o}\\ \Rightarrow x = {25^o}\end{array}\)
+)
\(\begin{array}{l}y + {70^o} + {60^o} = {180^o}\\ \Rightarrow y = {180^o} - {70^o} - {60^o}\\ \Rightarrow y = {50^o}\end{array}\)
+)
\(\begin{array}{l}z+ {90^o} + {55^o} = {180^o}\\ \Rightarrow z = {180^o} - {90^o} - {55^o}\\ \Rightarrow z = {35^o}\end{array}\)
18 tháng 9 2023
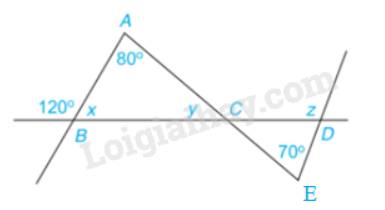
Ta có:
\(x + {120^o} = {180^o}\)( 2 góc kề bù)
\(\begin{array}{l} \Rightarrow x = {180^o} - {120^o}\\ \Rightarrow x = {60^o}\end{array}\)
Áp dụng định lí tổng các góc trong tam giác ABC, có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ \Rightarrow {80^o} + {60^o} + y = {180^o}\\ \Rightarrow y = {40^o}\end{array}\)
Ta có: \(\widehat {DCE} = y = {40^o}\)(đối đỉnh)
Áp dụng định lí tổng các góc trong tam giác CDE, có:
\(\begin{array}{l}\widehat C + \widehat D + \widehat E = {180^o}\\ \Rightarrow {40^o} + \widehat D + {70^o} = {180^o}\\ \Rightarrow \widehat D = {70^o}\end{array}\)
Mà \(\widehat D + z = {180^o}\)( 2 góc kề bù)
\( \Rightarrow z = {180^o} - {70^o} = {110^o}\)
15 tháng 10 2023
ta có x + 120* =180*(2 góc kề bù)
=> x= 180*-120*
= 60*
Ta có A+X+Y =180*
=> Y = 180*- A - X
= 180* - 80* - 60*
= 40*
ta có Y = ZCE = 40* (2 góc đối đỉnh)
Ta có Z = E + ZCE(định lý tổng 3 góc của TG )
=>Z = 70*+40*
=110*
9 tháng 9 2023
x=180-120-35=180-155=25 độ
y=180-70-60=50 độ
z=180-90-55=35 độ
QT
1
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
a) Vì m // n nên x = 135\(^\circ \)( 2 góc đồng vị) ; y = 80\(^\circ \) ( 2 góc so le trong)
b)
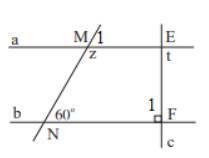
Vì a // b nên \(\widehat {{M_1}} = 60^\circ \) ( 2 góc đồng vị)
Mà \(\widehat {{M_1}} + z = 180^\circ \) ( 2 góc kề bù) nên z = 180\(^\circ \)- 60\(^\circ \)=120\(^\circ \)
Vì a // b nên \(\widehat {{F_1}} = t\) ( 2 góc so le trong), mà \(\widehat {{F_1}} = 90^\circ \) nên t = 90\(^\circ \)