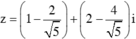Trong các số phức z thỏa mãn điều kiện |z – 1 – 2i| = 2, tìm số phức z có môđun nhỏ nhất.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan

CM
23 tháng 7 2019
Chọn C.
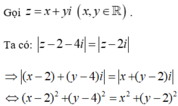
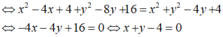
Do đó tập hợp các điểm biểu diễn số phức z là đường thẳng có phương trình x + y – 4 = 0
Mặt khác
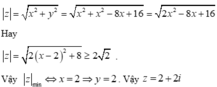
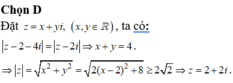
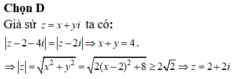
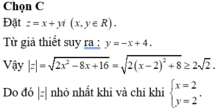

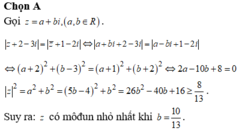



Chọn C.
Gọi z = x + yi và M (x; y) là điểm biểu diễn số phức.
Ta có : |z – 1 – 2i| = 2 hay ( x - 1) 2 + (y - 2)2 = 4
Đường tròn (C): ( x - 1)2 + (y - 2)2 = 4 có tâm I(1; 2). Đường thẳng OI có phương trình y = 2x
Số phức z thỏa mãn điều kiện và có môdun nhỏ nhất khi và chỉ khi điểm biểu diễn số phức đó thuộc đường tròn (C) và gần gốc tọa độ O nhất, điểm đó chỉ là một trong hai giao điểm của đường thẳng OI với (C), khi đó tọa độ của nó thỏa mãn hệ
Chọn nên số phức
nên số phức