Cho tứ diện ABCD có: AB = AC = AD, góc BAC bằng góc BAD bằng 60 o . Gọi M và N lần lượt là trung điểm của AB và CD.
Mặt phẳng (BCD) vuông góc với mặt phẳng
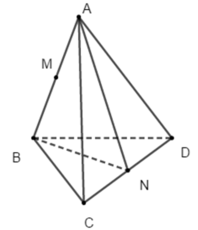
A. (CDM)
B. (ACD)
C. (ABN)
D. (ABC)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

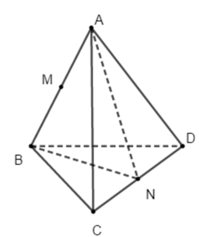
Các tam giác ABC và ABD là tam giác đều ⇒ tam giác ACD cân
⇒ BN ⊥ CD và AN ⊥ CD ⇒ góc ANB là góc của hai mặt phẳng (ACD) và (BCD)
Đáp án B

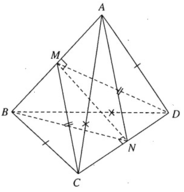
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.

Phương án A sai vì nếu CD ⊥ (ABD) thì CD ⊥ AD. Nhưng tam giác ACD cân tại A nên CD không thể vuông góc với AD
Phương án B sai vì tương tự như trên thì CD không thể vuông góc với AC
Phương án C đúng vì CD ⊥ AN (AN là đường trung tuyến của tam giác cân CAD tại A) và CD ⊥ MN ⇒ CD ⊥ (ABN)
Phương án D sai vì CD không vuông góc với MD do chứng minh trên.
Đáp án C

Loại phương án A và B vì BC và CD không phải là hình chiếu của CM trên (BCD)
Phương án C đúng vì :

Đáp án C

Đáp án A
Chọn hệ trục tọa độ Oxy
![]()
A D = 2 a tan 60 o = 2 a 3
Từ M kẻ MH song song với AC ta có MH =a
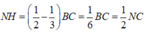
![]()
PT của mặt phẳng (BCD) là x 2 a + y 2 a + z 2 3 a = 1
Vậy khoảng cách từ
P
(
0
;
4
a
;
0
)
đến (BCD) là:
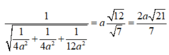

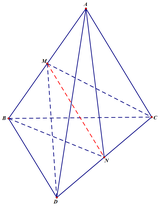
a, Do N là trung điểm của CD ⇒ N ∈ (ACD).
Ta có N ∈ (ABN).
Mặt khác: A ∈ (ACD) và A ∈ (ABN)
⇒ (ACD) \(\cap\) (ABN) = AN
b, Do N ∈ CD ⇒ N ∈ (CDM). Hiển nhiên : N ∈ (ABN)
Do M ∈ AB nên M ∈ (ABN). Hiển nhiên : M ∈ (CDM)
⇒ (ABN) \(\cap\) (CDM) = MN
Ta có CD ⊥ (ABN) (do BN ⊥ CD và AN ⊥ CD) ⇒ (BCD) ⊥ (ABN)
Đáp án C