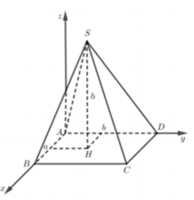
Cho hình chóp S.ABCD, đáy hình thang ABCD có đáy lớn AD. Trong các mệnh đề sau mệnh đề nào sai?
A. Hai mặt phẳng (SAC) và (SBD) cắt nhau
B. Hai mặt phẳng (SAB) và (SCD) cắt nhau
C. Hai mặt phẳng (SAD) và (SBC) không cắt nhau
D. Bốn điểm S, A, C, D cùng nằm trong một mặt phẳng

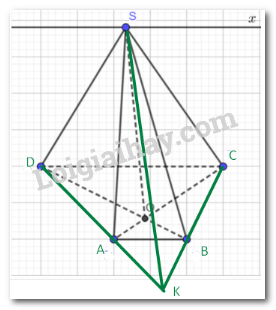
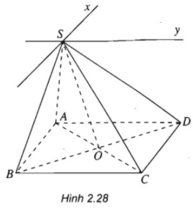
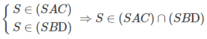
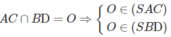
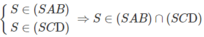
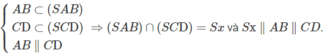

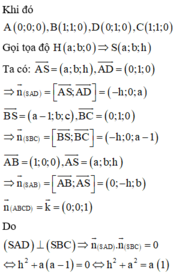
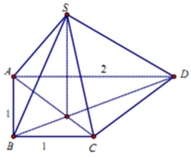
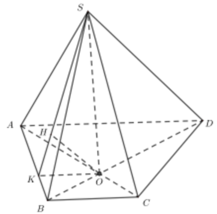

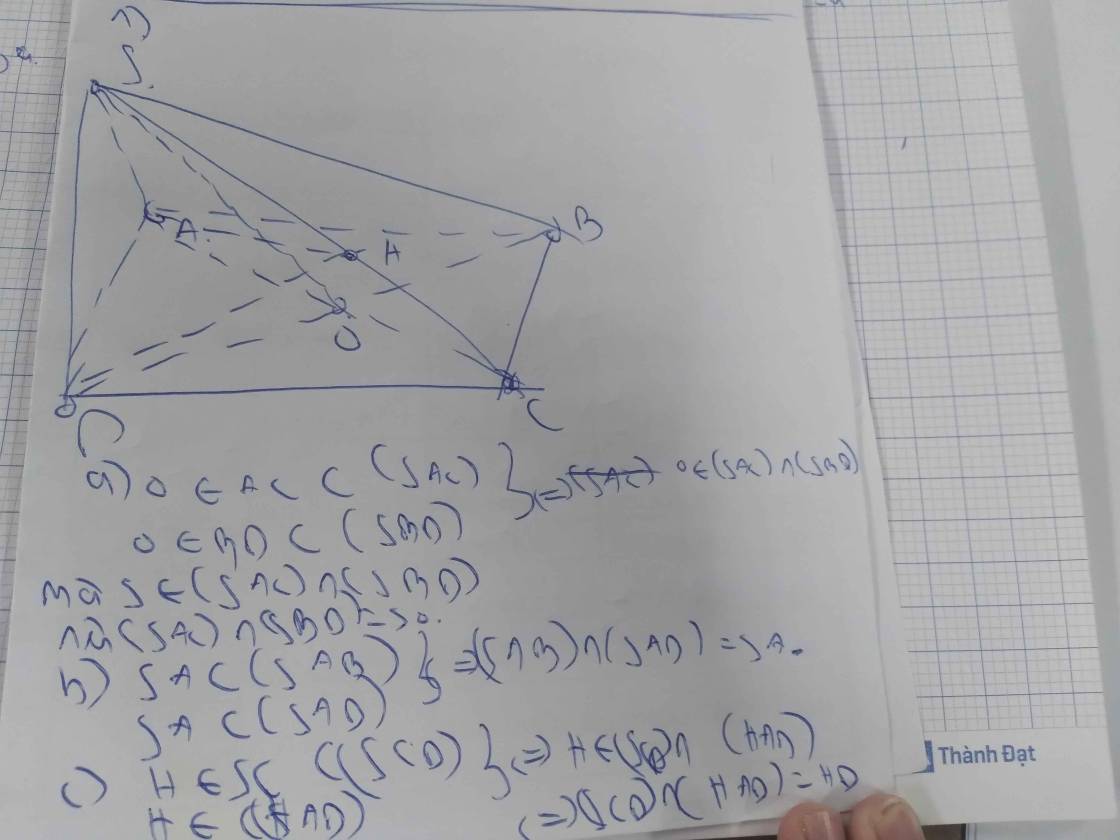

A. (SAC) ∩ (SBD) = SO
B. (SAB) ∩ (SCD) = SE
C. (SAD) ∩ (SBC) = xy
D. nếu S, A, C, D cùng nằm trong một mặt phẳng thì S ∈ (ACD) mâu thuẫn với giả thiết S.ABCD là hình chóp
Đáp án D