Cho tam giác ABC vuông tại A có BC = 8, C ^ = 30 ° . Diện tích của tam giác đó là?
A. 8 2
B. 8 3
C. 4 3
D. 4 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A.
(h.2.59) Trong tam giác ABC vuông tại A, ta có:
AC = BC.sin30 ° = a;
AB = BC.cos30 ° = a 3 .
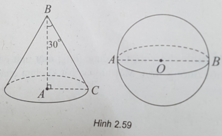
Diện tích toàn phần hình nón là:
S 1 = S xq + S đáy = πRl + πR 2 = πa . 2 a + πa 2 = 3 πa 2
Diện mặt cầu đường kính AB là:
S 2 = πAB 2 = π a 3 2 = 3 πa 2
Từ đó suy ra, tỉ số S 1 / S 2 = 1

Xét EAF và EAC có:
+chung đường cao hạ từ e
+AF = 1/3 AC
=> S EAF= 1/3 S EAC
Xét EAC và ABC có:
+Chung đường cao hạ từ C
+AE=3/4 AB
=>S EAC =3/4 S ABC
=> S EAC= (1/3 x 3/4) S ABC = 1/4 S ABC
Tương tự
S BED =1/8 S ABC
S CDF=1/3 S ABC
=> S DEF= S ABC -S BED -S CDF
= S ABC -1/4 S ABC -1/8 S ABC -1/3 S ABC
= 7/24 S ABC
= 7/24 x 1/2 x AB x AC
= 7/24 x 1/2 x 8 x 12 =14 (cm^2)
Xét EAF và EAC có:
+chung đường cao hạ từ e
+AF = 1/3 AC
=> S EAF= 1/3 S EAC
Xét EAC và ABC có:
+Chung đường cao hạ từ C
+AE=3/4 AB
=>S EAC =3/4 S ABC
=> S EAC= (1/3 x 3/4) S ABC = 1/4 S ABC
Tương tự
S BED =1/8 S ABC
S CDF=1/3 S ABC
=> S DEF= S ABC -S BED -S CDF
= S ABC -1/4 S ABC -1/8 S ABC -1/3 S ABC
= 7/24 S ABC
= 7/24 x 1/2 x AB x AC
= 7/24 x 1/2 x 8 x 12 =14 (cm^2)

Câu 1: Diện tích tam giác là: \(\frac{h_A.a}{2}=\frac{3.6}{2}=9\)(đvdt)
Câu 2: Diện tích tam giác là: \(\frac{1}{2}ab.\sin C=\frac{1}{2}.4.5.\sin60^o=5\sqrt{3}\)(đvdt)
Câu 2: Ta có: \(\hept{\begin{cases}c^2=a^2+b^2-2ab.\cos C\\a^2+b^2>c^2\end{cases}\Rightarrow c^2>c^2-2ab.\cos C\Leftrightarrow2ab.\cos C>0}\)
\(\Rightarrow\cos C>0\Rightarrow C< 90^o\)
Vậy C là góc nhọn

Chọn B.
Nửa chu vi của tam giác là p = (4 + 6 + 8) : 2 = 9
Áp dụng công thức Hê-rông
Suy ra: ![]()

Câu 9:
a: \(3\left(2x-3\right)+2\left(2-x\right)=-3\)
=>6x-9+4-2x=-3
=>4x-5=-3
=>4x=2
=>x=1/2
b: \(\Leftrightarrow6x^2+9x-6x^2+4x-15x+10=8\)
=>-2x+10=8
=>-2x=-2
=>x=1
d: \(\Leftrightarrow x^2+4x+4-x^2+4=0\)
=>4x+8=0
=>x=-2
Đáp án B
Áp dụng hệ thức về cạnh và góc trong tam giác vuông ta có: